NOTE: The required graph in Part I.B. of this lab is the same as that in Part I.C. of Lab 4.5. If you are doing both labs, and you have already produced the graph for Parts I.B. of Lab 4.5, you do not have to reproduce it for this lab. In your lab report, indicate where it is found in the Lab 4.5 lab report (e.g., ``Figure 1 of the Lab 4.5 lab report.'')
The SAS data set SASDATA.STATOPOLIS contains information on 100,000 households.1 For the purposes of this lab, these 100,000 households will constitute the population.
- A.
- Open SASDATA.STATOPOLIS in SAS/INSIGHT now
(Recall that to get into SAS/INSIGHT you choose Solutions: Analysis: Interactive Data Analysis
from any of the main SAS windows). You will see that
there are four variables in the data set:
- o
- HHSIZE: household size.
- o
- VALUEH: the value of the house.
- o
- H_INCOME: household income.
- o
- H_GENDER: gender of the head of the
household (0=female, 1=male)
- B.
- Do a distribution analysis on H_INCOME (by
choosing Analyze: Distribution ( Y )).
Notice that the density histogram has many bars. H_INCOME takes so many different values, it is easier to model its distribution using a density curve. To see what such a curve might look like, select Curves: Kernel Density then click OK. Print or save this histogram with the density curve for your lab report.
The Central Limit Theorem states that under very broad assumptions (the existence of a finite population variance), the distribution of the mean of a random sample from a population will be asymptotically normal. The implication of this, which has been borne out in practice, is that the more observations used to compute a mean, the closer to normal the distribution of that mean will be.
In this lab, you will take several random samples of different sizes. You will compute the mean of the data in each sample, and then you will pool your results with those of others in the class. The result will be a data set consisting of means from at least 100 random samples.
- A.
- Select the samples using the SAS macro
LAB4_6.2 The macro will select one simple
random sample each of sizes 5, 10, and 50. These
will be placed in the SAS data sets WORK.SAMP5A,
WORK.SAMP10A, and WORK.SAMP50A, respectively.
- B.
- Open each of the three samples in SAS/INSIGHT.
For each, compute the mean of H_INCOME. The easiest way
to do this is to choose Analyze: Multivariate ( Y X
) and input H_INCOME as the the Y variable. The mean
will appear in the Univariate Statistics box in the output
window. Record two copies of the values of the three
means: one for your lab report, and the other to give the
TA. Next term, the values will be input to the SAS data
set SASDATA.LAB4_6. Since this is a new lab, we have
already done the work of creating the data set. Go to Part
III to analyze it.
To see the Central Limit Theorem at work, you must look at the distributions of the means in the data set SASDATA.LAB4_6 to see if the distributions become more and more normal as more data values go into them. Specifically, for the variable H_INCOME, the distribution of means for samples of size 50 should be more normal than the distribution of means for samples of size 10, the distribution of means for samples of size 10 should be more normal than the distribution of means for samples of size 5, and the distribution of means for samples of size 5 more normal than the original population distribution.
- A.
- Open SASDATA.LAB4_6 in SAS/INSIGHT. This
data set contains the means of H_INCOME submitted by
the entire class. The values for the means of samples
of sizes 5, 10 and 50 are found under the variable
names MEAN5, MEAN10 and MEAN50. There is also a random
sample of the original H_INCOME values for
comparison. Obtain a distribution analysis on each of
these variables (by choosing Analyze:
Distribution ( Y )).
- B.
- You are now going to check the
normality of each. To do so, you need the
following facts:
- o
- If a random sample of size
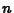is
drawn from a population having mean 
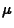and standard deviation 
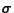, and if
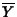is the mean of the random
sample, then 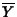has population
mean 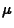and population standard
deviation
.
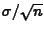- o
- The mean of the population of
H_INCOME values is
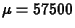, and the
standard deviation is
,
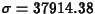both computed from the gamma density.
Therefore, population mean of MEAN5 is 57500
and the population standard deviation is
.
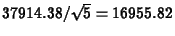Obtain the population mean and standard deviation for both MEAN10 and MEAN50.
- C.
- Now superimpose a
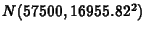density curve on the density histogram of
MEAN5. To do this, choose Curves:
Parametric Density. From the resulting
window,
- 1.
- Make sure the normal
distribution is selected.
- 2.
- Set the Method: to
Specification.
- 3.
- Set Mean/Theta: to
57500.
- 4.
- Set Sigma: to
16955.82.
Print or save the density histogram with the superimposed normal density curve for your lab report.
- D.
- Repeat C. for H_INCOME, MEAN10 and
MEAN50. Be sure to use the correct value of
Sigma: for each.
- E.
- As a second check on normality,
produce a normal quantile plot for
H_INCOME, MEAN5, MEAN10 and MEAN50. To do
this for MEAN5, proceed as follows:
- 1.
- Choose Curves: QQ Ref
Line.
- 2.
- From the resulting window,
make sure Method: is set to
Specification, Intercept
is set to 57500, and Slope
is set to 16955.8.2.
Print or save the normal quantile plot for your lab report.
- F.
- Repeat E. for H_INCOME, MEAN10, and MEAN50.
In your lab report, be sure to include the following:
- The graph from I.B. (if you are not already
including it for Lab 4.5).
- The values of the three sample means
from samples of size 5, 10 and 50 (see Part II.B.).
- The values of 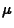and
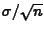for H_INCOME, MEAN5, MEAN10, and
MEAN50 (see Part III.B.).
- Density histograms with superimposed
normal density curves for H_INCOME, MEAN5, MEAN10,
and MEAN50 (see Part III.C.).
- Normal quantile plots with superimposed
reference lines for H_INCOME, MEAN5, MEAN10, and
MEAN50 (see Part III.E.).
- Analysis of how the results you have
obtained demonstrate the Central Limit Theorem.