The SAS data set SASDATA.STATOPOLIS contains information on 100,000 households.1For the purposes of this lab, these 100,000 households will constitute the population.
- A.
- Open SASDATA.STATOPOLIS in SAS/INSIGHT now (Recall that
to get into SAS/INSIGHT you choose Solutions: Analysis: Interactive Data
Analysis from any of the main SAS windows). You
will see that there are four variables in the data set:
- o
- HHSIZE: household size.
- o
- VALUEH: the value of the house.
- o
- H_INCOME: household income.
- o
- H_GENDER: gender of the head of the household (0=female, 1=male)
- B.
- Do a distribution analysis on H_INCOME (by
choosing Analyze: Distribution ( Y )).
Notice that the density histogram has many bars. H_INCOME takes so many different values, it is easier to model its distribution using a density curve. To see what such a curve might look like, select Curves: Kernel Density then click OK. Print or save this histogram with the density curve for your lab report.
By using some statistical trickery, we have managed to come up with a standard density curve that models the population closely. It's called a gamma distribution with parameters
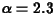 and
and
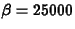 . The density curve for this gamma
distribution is
. The density curve for this gamma
distribution is
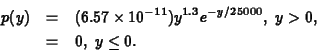
The gamma distribution is common in probability and statistics, and probabilities involving it may be computed using the SAS macro NPROBS, which you will do in Part II of this lab. In the rest of the lab, we will assume this gamma distribution is the population distribution.
In this part of the lab, you will take two random samples from the population: one of size 5, and one of size 50. You will use the data in the size 5 and size 50 samples to obtain a range of values that with high probability contains at least 99% of all household incomes in the population using a tolerance interval. After computing these quantities on the data you sampled, you will pool your results with those of others in the class. This pooled data will be used in this lab next term to evaluate the performance of the three kinds of intervals Since this is a new lab, we have created a pooled data set (under the name SASDATA.LAB5_3TI) for you to analyze in Part III of this lab.
- A.
- Select the samples by running the SAS macro
LAB5_3.2 The samples
of size 5 and 50 will be written to the SAS data sets
WORK.SAMP5 and WORK.SAMP50,
respectively.
- B.
- Open each of the samples in SAS/INSIGHT. For the
samples of size 5 and 50, compute a normal theory level
0.95 tolerance interval for a proportion 0.99 of the
population values. Use formula (5.27), p. 269 of the
text, or you can use the SAS macro NORTOL.
Once you have obtained the tolerance interval, check whether it really contains at least 99% of all population household incomes. To do this, use the SAS macro NPROBS. The following illustrates how:
Suppose the tolerance interval you obtained has endpoints 5,000 and 190,000. Access the macros by selecting Solutions: EIS/OLAP Application Builder: Applications: Run Private Applications. Select the macro NPROBS. In the macro window, choose the gamma distribution with parameters
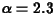 and
and 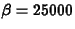 , and interval endpoints
, and interval endpoints 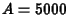 and
and 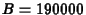 . The resulting value is 0.9849,
meaning that 98.49% of all household incomes lie
between $5000 and $190000. therefore, this
tolerance interval fails to contain at least 99% of
all household incomes in the
population.3
. The resulting value is 0.9849,
meaning that 98.49% of all household incomes lie
between $5000 and $190000. therefore, this
tolerance interval fails to contain at least 99% of
all household incomes in the
population.3
For each of the data sets your group generates, write down the tolerance interval, the proportion of the population values it contains, and whether it contains at least 99% of all household incomes in the population. Submit the results to the TA. The values for the entire class will be input to a SAS data set for use next term. Because this is a new lab, we have created a data set of 100 observations for you. You will find it in the SAS data set SASDATA.LAB5_3TI.
Open the SAS data set SASDATA.LAB5_3TI in SAS/INSIGHT now (Recall that to get into SAS/INSIGHT you choose Solutions: Analysis: Interactive Data Analysis from any of the main SAS windows). The data set has the following variables:
- o
- LTOL5: The lower tolerance limit from the
sample of size 5.
- o
- UTOL5: The upper tolerance limit from the
sample of size 5.
- o
- PROP5: The proportion of population values
covered by the tolerance interval from the
sample of size 5.
- o
- INTOL5: 1 if the tolerance interval from the
sample of size 5 includes at least 99% of the
population values; 0 otherwise.
- o
- LTOL50: The lower tolerance limit from the
sample of size 50.
- o
- UTOL50: The upper tolerance limit from the
sample of size 50.
- o
- PROP50: The proportion of population values
covered by the tolerance interval from the
sample of size 50.
- o
- INTOL50: 1 if the tolerance interval from
the sample of size 50 includes at least 99% of the
population values; 0 otherwise.
Have a look at these to familiarize yourself with them.
- A.
- Run the SAS Macro L5_3TI5. This will
produce a plot of the tolerance intervals in the
SASDATA.LAB5_3TI data set based on the samples of
size 5. The plot has two parts: one showing the
intervals and the second showing the proportion of
population values contained within each interval.
Both parts are color coded: green indicates that
at least 99% of the population values lie between
the endpoints of the interval, and red indicates
the percentage is less than 99. The macro also
computes the mean width of the tolerance
intervals. Print the plot and write down the
values of the mean widths for submission with your
lab report.
- B.
- Run the SAS Macro L5_3TI50. This macro
produces the same output as L5_3TI5, but for
samples of size 50. Print the plot and write down
the values of the mean widths for submission with
your lab report.
Two issues in the performance of tolerance intervals are coverage and precision.
- 1.
- For tolerance intervals, coverage means
that the interval contains at least the
desired proportion of population values
(here the proportion is 0.99). Calculate the
coverage from the confidence interval plots
for sample sizes 5 and 50 for submission
with your lab report. Are they both close to
the nominal coverage of 0.95? To each
other?
- 2.
- As it does for the other types of
intervals, precision of tolerance intervals
refers to interval width. Compare the mean
interval widths for both sample sizes.
- C.
- Based on what you have seen in parts III.
A. and B., summarize how sample size affects coverage
and precision of the tolerance intervals.
The population distribution of H_INCOME is nonnormal. In fact, it's pretty heavily right skewed. For some types of intervals this will make a large difference and for some it will make little difference. Do you think the performance of the tolerance intervals might have been affected by the nonnormality of the population distribution? In what way were they affected? Explain your choices.
In your lab report, be sure to include the following:

- Histogram of population values with
density curve (I.B.).

- For the tolerance intervals you
compute by hand: (1) The sample size (5 or 50) (2)
The interval (3) The proportion of population
values it contains (4) Whether it contains at least
99% of all population values. (II.B.).

- Two plots, mean widths for tolerance
intervals, and coverage (III.B.).

- Overall summary of findings (III.C.).