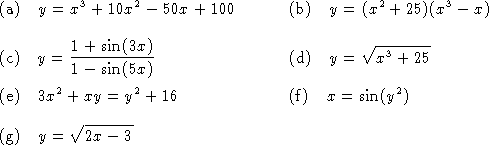
2. Compute the following limits.
;
;
.
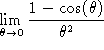4. Consider the function
5.
Consider the function 
.
(a) Show that the equation f(x) = 0 has at least
one root in the interval [1,2].
(b)
Do three steps of Newton's method to approximate the
root that lies between x=1 and x=2.
Use 
as your initial guess.
6.
The radius of a spherical ball is measured as 1.4 cm with a
maximum error of 0.01 cm. Estimate the maximum resulting
error in the calculated volume. Estimate the maximum error
allowed in the measurement of the radius if the computed
volume must be correct to within 0.01 cubic centimeters.
7.
If the people of Babylon could approximate square roots,
you should be able to approximate cube roots.
Describe your method and show how to use it to approximate the
cube root of 65.
8.
Give an argument to show that the polynomial
has exactly one real root.
9.
A light is at the top of a pole 50 feet high. A ball is dropped from the
same height 30 feet from the light. You may assume that
the ball falls a distance 
feet in t
seconds. How fast is the shadow of the ball moving along the ground
1/2 second after the ball is dropped?
10.
Your job is to design a cylindrical box to hold Quacker Oats.
The material for the side of the cylinder costs 5 cents per square foot
while the material for the circular caps costs
20 cents per square foot.
(a) Find the dimensions of the cheapest box that Quacker Oats
can make if the box must hold exactly 1 cubic foot of oats.
In particular, show that for the optimal box, the height is
exactly eight times the radius.
(b) Find the largest box that the Quacker Folks can make if they
budget exactly 
for each box. Once
again, show that the height of the optimal box is exactly eight times
the radius. As always, justify your answer.
11. A walk-in shed is to have a square base, a flat roof, and a volume of 450 cubic feet. The materials cost $5 per square foot for the floor, $4 per square foot for the roof, and $10 per square foot for the sides, including the side into which the door is cut and the door itself. Determine suitable dimensions for the shed.
12. A new style of rectangular aquarium will have a volume of 1350 cubic inches, with a length to be twice the width. Plastic for the base costs $0.03 per square inch and glass for the sides costs $0.10 per square inch. (The top will be left open.) Determine the dimensions that will make the price of the aquarium the most competitive in the marketplace. 13. A contractor plans to build a rectangular patio, with area equal to 98 square feet, behind his house. Fencing and shrubbery will be used to give privacy. The fencing material for the sides costs $50 per foot and the shrubbery along the back costs $8 per foot. Find the best dimensions assuming that the contractor is very concerned about cost.
Take a look at the solutions
Back to the Bridge Projects Home Page
