Building Bridges in the First Two Years
1. Find dy/dx if
.
.
.
.
.
.
.
.
;
.
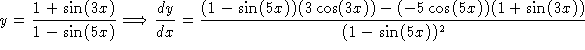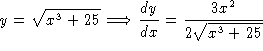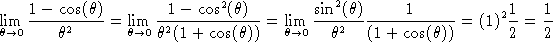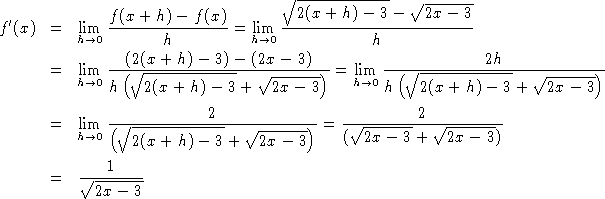
4. Consider the function
and a point: (2,f(2)) = (2,-8),
so the equation for the tangent line is (y+8) = 15(x-2) or y = 15x -38 .
is positive for x < -3 and x > 1
so f(x) is increasing here.
is negative for -3 < x < 1
so f(x) is decreasing here.
.
(a) Show that the equation f(x) = 0 has at least
one root in the interval [0,2].
The function is continuous on the interval and it changes sign.
It follows from the intermediate value theorem that it must
equal zero in the interval.
(b)
Do three steps of Newton's method to approximate the
root that lies between x=1 and x=2.
Use 
as your initial guess.
The basic iteration formula is
Make a table:
The approximate root after three steps is x = 1.5214. 6. The radius of a spherical ball is measured as 1.4 cm with a maximum error of 0.01 cm. Estimate the maximum resulting error in the calculated volume. Estimate the maximum error allowed in the measurement of the radius if the computed volume must be correct to within 0.01 cubic centimeters. To estimate the error, use
The numbers give you 
cubic centimeters as the maximum error in the computed volume.
To estimate the maximum allowable measurement error, turn the above computation
around and solve
So you need 
centimeters.
7.
Use Newton's method to solve the equation 
where
N is the number that you want to ``un-cube''. You obtain the
following algorithm:
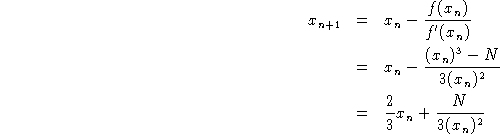
If you apply this with N = 65, starting at 
, you should
converge to 
in three steps.
8.
Give an argument to show that the polynomial
has exactly one real root.
To show that is has at least one root, note that f(0) is negative
and f(2) is very positive. (Any values for x which give a
sign change for f are sufficient.) Continuity and the intermediate
value theorem guarantee one root in the interval [0,2].
To argue that there is at most one root, note that
so the function is always increasing. In fact, it is strictly
increasing for 
. The only way that an increasing
function can have more than one root is for the function
to be constant on an interval, but the given function
is not constant on any interval.
9.
A light is at the top of a pole 50 feet high. A ball is dropped from the
same height 30 feet from the light. You may assume that
the ball falls a distance 
feet in t seconds.
How fast is the shadow of the ball moving along the ground 1/2 second
after the ball is dropped?
Let x(t) denote the location of the shadow (distance from the wall in feet)
at time t and let h(t) denote the height of the ball at time t.
You are given that 
so dh/dt = -32 t. Your goal is
to compute dx/dt.
Relate x and h (using similar triangles):
Relate the rates (differentiate implicitly):
Plug in the numbers (t = 1/2) to conclude that the shadow is moving at dx/dt = (375/4)(-16) = -1500 feet per second. (Negative because it moves toward the wall.) 10. Your job is to design a cylindrical box to hold Quacker Oats. The material for the side of the cylinder costs 5 cents per square foot while the material for the circular caps costs 20 cents per square foot. There are two basic equations involved in this problem:
(a) Find the dimensions of the cheapest box that Quacker Oats can make if the box must hold exactly 1 cubic foot of oats. In particular, show that for the optimal box, the height is exactly eight times the radius. The volume is fixed (equal to 1) and the goal is to minimize the cost. Differentiate to obtain an expression for dh/dr:
Now differentiate C with respect to r and use this expression for dh/dr:
Now set dC/dr = 0 to find the critical point: r = h/8.
To get actual numbers, use 
,
so 
feet and
feet. (One very tall box of oats!)
The minimum cost is about 44 cents per box.
This problem has no natural endpoints, but the sign of dC/dr tells you that C is decreasing for r < h/8 and increasing for r > h/8, hence r = h/8 gives the absolute minimizer for the cost. Note: you could also use V=1 to eliminate h from the cost equation and minimize
So
Now go back and solve for h, compute the volume,
and explain why this is the minimizer that you want.
(b) Find the largest box that the Quacker Folks can
make if they budget exactly 
for each box.
Once again, show that the height of the optimal box is
exactly eight times the radius.
As always, justify your answer.
The cost is fixed (equal to 200 cents) and the goal is to
maximize the volume.
From part (a), you know that the cheapest box for a fixed volume
has h = 8r. This is still the best solution if you seek to
maximize the volume for a fixed price. So use
to obtain 
so that 
feet.
Then 
feet
and the maximum volume is about 9.711 cubic feet.
(You get a big box of oats for !)
11. See the Maple worksheet.
12. See the Maple worksheet.
Back to the Bridge Projects Home Page