Maple has several useful functions for working with vectors. This lab provides a brief introduction to the most basic such commands. All of the commands used in this lab come from the Maple linalg package, which must be loaded before any of the commands can be used.
Here is a list of the Maple functions we will be using from this package. Note that these functions form only a small subset of the package, which is designed primarily for linear algebra. Examples for some of the commands are given below, more examples can be found in the help screens for each command. Several of these commands appeared in the previous lab, so you might want to refer back to it.
The first set of examples below demonstrates how to compute linear combinations of vectors, dot and cross products, magnitudes, and vector components for fixed vectors.
> with(linalg):
Warning: new definition for norm Warning: new definition for trace
> a := vector([2,13,-6]);
> b := vector([5,-4,17]);
> add(a,b);
> evalm(5*a-2*b);
> dotprod(a,b);
> crossprod(a,b);
> crossprod(b,a);
> dotprod(a,crossprod(a,b));
The next two commands show two different ways to compute the magnitude
of a vector. The first way uses the norm
command. Note the 2 as the second argument of the command. This
2 has to be there, or else Maple uses a different norm
than the one we want. The second way, using the fact that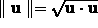 
, is preferred for
reasons given in the examples below dealing with arbitrary vectors.
> norm(a,2);
> sqrt(dotprod(a,a));
The final example for fixed vectors shows two methods for computing
the vector component
of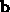 
in the direction of 
. The first method computes a
unit vector in the direction of 
and then applies the formula
in the book. The second method uses
the equivalent formula
> a_unit:= evalm(a/sqrt(dotprod(a,a)));
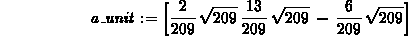
> comp_a1 := evalm(dotprod(b,a_unit)*a_unit);
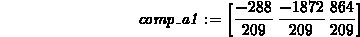
> comp_a2 := evalm(dotprod(b,a)/dotprod(a,a)*a);
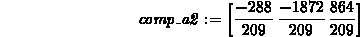
In the next set of examples two arbitrary three-dimensional vectors,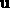 
and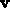 
, are defined and then these vectors are used to
prove the vector
identity
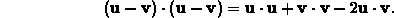
Note that when defining an arbitrary vector, that is, a vector whose
components are all variables, you only have to give the dimension of
the vector to the vector command. For example, to define a
four-dimensional arbitrary vector called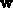 
the command would
be w:= vector(4);.
> u := vector(3);
> v := vector(3);
The next two commands show the two ways of computing the magnitude of
an arbitrary vector. Note the absolute value signs appearing in the
output of the norm command. These appear because Maple is
allowing the components of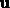 
to be complex numbers. The
problem is that there is not a simple way to tell Maple that the
components of 
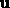are real numbers. The absolute value signs
cause problems in proving vector identities involving real vectors, so
you should use the square root of the dot product of a vector with
itself to compute the magnitude.
> norm(u,2);
> sqrt(dotprod(u,u));
The next few commands show how to prove the vector identity given above. The strategy is to compute both sides of the equation and then compare them. If they are identical, then the equation holds.
> eq1 := dotprod(evalm(u-v),evalm(u-v));
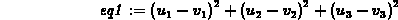
> expand(eq1);
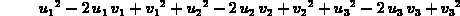
> eq2 := dotprod(u,u)+dotprod(v,v)-2*dotprod(u,v);
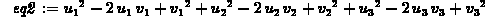
> simplify(eq1-eq2);
