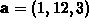 and
and 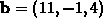 .
.
-
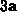 .
.
-
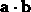 .
.
-
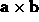 .
.
-
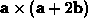 .
.
-
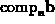 .
.
-
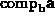 .
.
 and
and 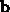 are the vectors from the previous
exercise, explain why it is true that
are the vectors from the previous
exercise, explain why it is true that
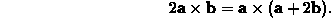
Note - just computing both sides of the equation and comparing is not a sufficient explanation. Your explanation must include references to properties of the cross product.
 perpendicular to
perpendicular to 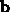 such that
such that

where 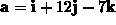 and
and 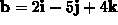 .
.
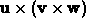 is not equal to
is not equal to 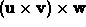 . Remember
that just showing that the results are not the same for specific fixed
vectors is not
enough. Instead, you should do the calculations with arbitrary
three-dimensional vectors.
. Remember
that just showing that the results are not the same for specific fixed
vectors is not
enough. Instead, you should do the calculations with arbitrary
three-dimensional vectors.
 is perpendicular to
is perpendicular to
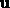 and perpendicular to
and perpendicular to 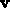 , where
, where 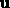 and
and 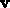 are arbitrary three-dimensional vectors.
are arbitrary three-dimensional vectors.
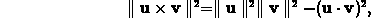
where 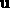 and
and 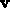 are arbitrary three-dimensional vectors, and
then explain how this identity implies the equation
are arbitrary three-dimensional vectors, and
then explain how this identity implies the equation
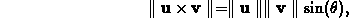
where 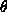 is the angle between
is the angle between 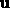 and
and 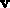 .
.