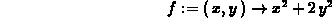Next: Exercises
Up: Curves on surfaces
Previous: Purpose
One problem that comes up again and again in engineering and science
is how to graphically represent functional relationships between more
than two variables. The basic problem is one of trying to represent
objects in three (or more) dimensions as two-dimensional plots. You
have already had experience with Maple's plot3d command, which
allows you to view a two-dimensional representation of a surface in
three dimensions from various angles. This is not the only
representation method, however. Another extremely useful method
involves plotting what are known as the contours.
Suppose 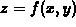 is the equation of a
surface in three dimensions and C is a
constant. The solution of the equation
is the equation of a
surface in three dimensions and C is a
constant. The solution of the equation 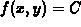 can be visualized
graphically by plotting the function together with the plane z=C.
The curve generated by this intersection is often referred to as a
contour. Note that this curve lies on the surface.
For example, the intersection of the two surfaces displayed by the
maple command
can be visualized
graphically by plotting the function together with the plane z=C.
The curve generated by this intersection is often referred to as a
contour. Note that this curve lies on the surface.
For example, the intersection of the two surfaces displayed by the
maple command
> plot3d({x^2+y^2,4},x=-3..3,y=-3..3);
would be the solution of the equation 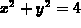 .
.
There are several cases where it is important to be able to find the
curves 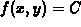 as the parameter C is varied, including the
following.
as the parameter C is varied, including the
following.
- On topographical maps, the function is the altitude. By looking
at the contours on such a map, you can determine how much climbing and
descending you would have to do on a hike.
- Contours of pressure are often used by meteorologists as a way of
locating fronts.
- Contours of temperature, velocity, field intensity, etc., are
often used in science and engineering.
In fact, drawing the contours of a function 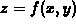 in the x-y
plane is another way of representing a surface in two dimensions. That
is, given the contour lines you should be able to reconstruct the
surface and vice-versa. There are several ways you can get Maple to
generate the contours on a plot generated with the plot3d
command. One way is with the style=CONTOUR option, as in the
following example.
in the x-y
plane is another way of representing a surface in two dimensions. That
is, given the contour lines you should be able to reconstruct the
surface and vice-versa. There are several ways you can get Maple to
generate the contours on a plot generated with the plot3d
command. One way is with the style=CONTOUR option, as in the
following example.
> plot3d(x^2+y^2,x=-2..2,y=-2..2,style=CONTOUR);
However, it is probably easier to generate the contours after you have
used plot3d to render the surface by using the Contours
and Patch and Contour options in the Style menu in the
Maple 3D plotting window. One thing to note is that Maple plots the
contours right on the surface. Usually, by a contour plot one means
the projection of the contour curves onto the x-y plane. To see
this in Maple, just view the plot from above or below. That is, rotate
the surface until you are viewing it along the z axis.
As noted above, contours are an example of curves on surfaces. In
fact, they are the curves on the surface along which the z value is
constant. They are one example of a slice through a surface. Another
important example of a slice through a surface in three dimensions is
the curve generated by fixing the value of one of the variables and
allowing the other one to vary. For example, suppose we were
considering the function 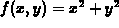 . Then the slice through
the surface
. Then the slice through
the surface 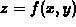 with y fixed at 1 would be obtained by
plotting the graph of
with y fixed at 1 would be obtained by
plotting the graph of 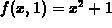 in the x-z plane.
in the x-z plane.
Slices of this type are useful in helping to visualize a surface and
also to get information on how the value of 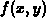 changes as one of
the variables is held fixed and the other is changed. In the old days,
plotting slices was one way to help visualize surfaces in three
dimensions. However, this use of slices has become less important as
technology has made it much easier to plot surfaces directly.
changes as one of
the variables is held fixed and the other is changed. In the old days,
plotting slices was one way to help visualize surfaces in three
dimensions. However, this use of slices has become less important as
technology has made it much easier to plot surfaces directly.
In this lab, we are mainly interested in these slices as curves
on the surface and our real goal is to use curves on surfaces to
investigate the behavior of functions 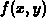 near some fixed point
on the surface. For example, suppose we had a function
near some fixed point
on the surface. For example, suppose we had a function 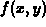 that
modeled the cost of a process and that x and y represented process
variables that we could change in small increments. If we wanted to
change them to decrease the cost, then it would be very helpful to
know how to change them to decrease the cost the most.
that
modeled the cost of a process and that x and y represented process
variables that we could change in small increments. If we wanted to
change them to decrease the cost, then it would be very helpful to
know how to change them to decrease the cost the most.
To solve this problem we need a way of measuring how the function
changes as the independent variables change. We saw in class that the
two partial derivatives of 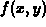 can be used to measure how the
function changes as one of the variables is changed and the other is
held fixed. The following definition describes a way to compute the
instantaneous rate of change of
can be used to measure how the
function changes as one of the variables is changed and the other is
held fixed. The following definition describes a way to compute the
instantaneous rate of change of 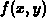 in any direction.
in any direction.
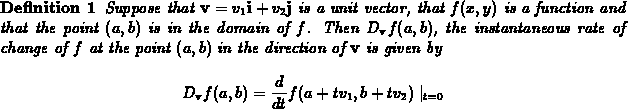
We will provide some examples below of how to compute these rates of
change, usually called directional derivatives, but first we want to
try to understand what is going on geometrically. First, we consider
the parametric curve in the plane given by 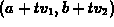 . This
curve is, in fact, a straight line and we know from our earlier work
that this line passes through the point
. This
curve is, in fact, a straight line and we know from our earlier work
that this line passes through the point 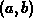 at t=0 and that
at t=0 and that
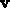 is a vector in the direction of the line. Second, the
parametric curve in three dimensions given by
is a vector in the direction of the line. Second, the
parametric curve in three dimensions given by
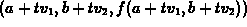 is a curve that lies on the
surface. In fact, it is the curve obtained by projecting the curve in
the x-y plane onto the surface and can be thought of as a
generalized slice.
is a curve that lies on the
surface. In fact, it is the curve obtained by projecting the curve in
the x-y plane onto the surface and can be thought of as a
generalized slice.
To help you visualize these generalized slices a Maple procedure
called SurfLoop has been written. What SurfLoop does is
project any curve in the x-y onto a surface and then plot the
resulting curve, colored green for identification, and the surface on
the same plot. Contours are also
provided. To prevent the curve from being hidden, the options in the
Style and Color menu in the plot window are disabled and
will not change the appearance of the plot. Axes, however, can be
added to the plot. As an option you can
also include the curve in the x-y plane in the plot. The
SurfLoop command is part of the CalcP package, which must be
loaded first.
The following examples deal with the simple function 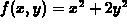 . The first example is of the slice
. The first example is of the slice 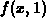 , the second is
of the slice
, the second is
of the slice 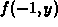 . The third example is also of the slice
. The third example is also of the slice
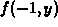 , but is set up so that the curve passes through the point
x=-1, y=1 at t=0. The fourth example presents a generalized slice
passing through the origin in the direction of the line y=x.
, but is set up so that the curve passes through the point
x=-1, y=1 at t=0. The fourth example presents a generalized slice
passing through the origin in the direction of the line y=x.
> with(CalcP):
> f := (x,y) -> x^2+2*y^2;
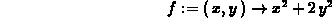
> SurfLoop(f(x,y),x=-2..2,y=-2..2,[t,1],t=-2..2);
> SurfLoop(f(x,y),x=-2..2,y=-2..2,[-1,t],t=-2..2);
> SurfLoop(f(x,y),x=-2..2,y=-2..2,[-1,1+t],t=-3..1);
> SurfLoop(f(x,y),x=-2..2,y=-2..2,[t/sqrt(2),t/sqrt(2)],t=-2..2);
The next examples show how to calculate the directional derivatives
for the generalized slices given above.
> subs(t=0,diff(f(t,1),t));

> subs(t=0,diff(f(-1,t),t));

> subs(t=0,diff(f(-1,1+t),t));

> subs(t=0,diff(f(t/sqrt(2),t/sqrt(2)),t));




Next: Exercises
Up: Curves on surfaces
Previous: Purpose
William W. Farr
Wed Apr 12 16:40:36 EDT 1995
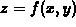 is the equation of a
surface in three dimensions and C is a
constant. The solution of the equation
is the equation of a
surface in three dimensions and C is a
constant. The solution of the equation 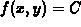 can be visualized
graphically by plotting the function together with the plane z=C.
The curve generated by this intersection is often referred to as a
contour. Note that this curve lies on the surface.
For example, the intersection of the two surfaces displayed by the
maple command
can be visualized
graphically by plotting the function together with the plane z=C.
The curve generated by this intersection is often referred to as a
contour. Note that this curve lies on the surface.
For example, the intersection of the two surfaces displayed by the
maple command
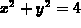 .
.
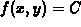 as the parameter C is varied, including the
following.
as the parameter C is varied, including the
following.
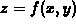 in the x-y
plane is another way of representing a surface in two dimensions. That
is, given the contour lines you should be able to reconstruct the
surface and vice-versa. There are several ways you can get Maple to
generate the contours on a plot generated with the plot3d
command. One way is with the style=CONTOUR option, as in the
following example.
in the x-y
plane is another way of representing a surface in two dimensions. That
is, given the contour lines you should be able to reconstruct the
surface and vice-versa. There are several ways you can get Maple to
generate the contours on a plot generated with the plot3d
command. One way is with the style=CONTOUR option, as in the
following example.
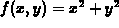 . Then the slice through
the surface
. Then the slice through
the surface 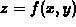 with y fixed at 1 would be obtained by
plotting the graph of
with y fixed at 1 would be obtained by
plotting the graph of 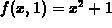 in the x-z plane.
in the x-z plane.
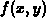 changes as one of
the variables is held fixed and the other is changed. In the old days,
plotting slices was one way to help visualize surfaces in three
dimensions. However, this use of slices has become less important as
technology has made it much easier to plot surfaces directly.
changes as one of
the variables is held fixed and the other is changed. In the old days,
plotting slices was one way to help visualize surfaces in three
dimensions. However, this use of slices has become less important as
technology has made it much easier to plot surfaces directly.
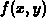 near some fixed point
on the surface. For example, suppose we had a function
near some fixed point
on the surface. For example, suppose we had a function 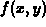 that
modeled the cost of a process and that x and y represented process
variables that we could change in small increments. If we wanted to
change them to decrease the cost, then it would be very helpful to
know how to change them to decrease the cost the most.
that
modeled the cost of a process and that x and y represented process
variables that we could change in small increments. If we wanted to
change them to decrease the cost, then it would be very helpful to
know how to change them to decrease the cost the most.
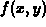 can be used to measure how the
function changes as one of the variables is changed and the other is
held fixed. The following definition describes a way to compute the
instantaneous rate of change of
can be used to measure how the
function changes as one of the variables is changed and the other is
held fixed. The following definition describes a way to compute the
instantaneous rate of change of 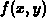 in any direction.
in any direction.
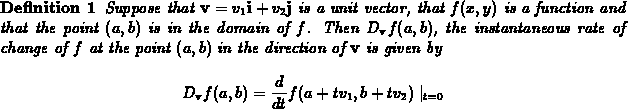
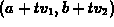 . This
curve is, in fact, a straight line and we know from our earlier work
that this line passes through the point
. This
curve is, in fact, a straight line and we know from our earlier work
that this line passes through the point 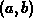 at t=0 and that
at t=0 and that
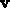 is a vector in the direction of the line. Second, the
parametric curve in three dimensions given by
is a vector in the direction of the line. Second, the
parametric curve in three dimensions given by
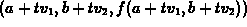 is a curve that lies on the
surface. In fact, it is the curve obtained by projecting the curve in
the x-y plane onto the surface and can be thought of as a
generalized slice.
is a curve that lies on the
surface. In fact, it is the curve obtained by projecting the curve in
the x-y plane onto the surface and can be thought of as a
generalized slice.
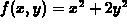 . The first example is of the slice
. The first example is of the slice 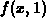 , the second is
of the slice
, the second is
of the slice 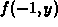 . The third example is also of the slice
. The third example is also of the slice
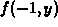 , but is set up so that the curve passes through the point
x=-1, y=1 at t=0. The fourth example presents a generalized slice
passing through the origin in the direction of the line y=x.
, but is set up so that the curve passes through the point
x=-1, y=1 at t=0. The fourth example presents a generalized slice
passing through the origin in the direction of the line y=x.