


Next: Machine Tool Wear
Up: No Title
Previous: Space Probe Rescue
The date is 1750 and Baron Munchausen, the scourge of Thuringia, has accused you of being a spy for the nearby state of Hesse. He has expressed a willingness to have you shot without trial, but has also said that he might change his mind if you can solve a problem that has baffled his gunnery officers. Based on your calculus expertise (and the fact that your life is on the line) you agree to try.
The Baron's problem appears to be relatively simple. It is well known that an angle of 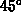 provides the greatest projectile range when the ground is flat. However, this angle does not seem to work as well if the Baron's artillery batteries are forced to fire uphill or downhill. The Baron wants to know what the optimum angle is in these cases.
provides the greatest projectile range when the ground is flat. However, this angle does not seem to work as well if the Baron's artillery batteries are forced to fire uphill or downhill. The Baron wants to know what the optimum angle is in these cases.
You, with your great knowledge of projectile trajectories and calculus, immediately begin to set the problem up. You first realize that setting up your coordinates as in Figure  will make it easier, because
will make it easier, because 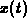 will be the distance that the Baron is interested in at the value of t where
will be the distance that the Baron is interested in at the value of t where 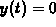 . In setting up your coordinates this way, you introduce two angles,
. In setting up your coordinates this way, you introduce two angles, 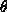 and
and 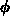 where
where 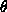 is the angle between the cannon and the ground and
is the angle between the cannon and the ground and 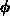 is the angle the ground makes with the horizontal.
is the angle the ground makes with the horizontal.
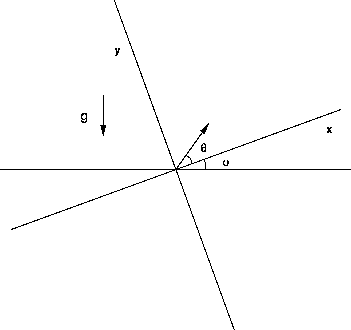
Figure: Coordinate System.
Given this coordinate system, you derive the following set of differential equations

and initial conditions

where 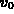 is the initial velocity of the projectile.
is the initial velocity of the projectile.
Your assignment is to find the angle 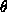 that gives the maximum range for each value of
that gives the maximum range for each value of 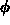 . In writing your report, the following points must be addressed.
. In writing your report, the following points must be addressed.
- First demonstrate how the differential equations and initial conditions were derived. You are free to use another coordinate system, but then you must demonstrate how to derive the equations in your coordinate frame.
- Solve the differential equations to obtain the trajectory
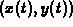 . Note that the variables
. Note that the variables 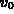 ,
, 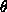 , and
, and 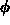 will appear as parameters in your solution.
will appear as parameters in your solution.
- You must also describe how you found the angle
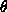 that gives maximum range for a given angle
that gives maximum range for a given angle 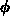 . A plot of
. A plot of 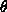 versus
versus 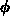 should be provided for the use of the Baron's field officers.
should be provided for the use of the Baron's field officers.
Schedule for Project 2
- Friday, February 21. Project handed out.
- Friday, February 28. Draft report due.
- Monday, March 2. Draft reports returned.
- March 2 and 3. Meetings with me to discuss the draft reports.
- March 5. Final reports due.



Next: Machine Tool Wear
Up: No Title
Previous: Space Probe Rescue
William W. Farr
Wed Jul 26 13:43:32 EDT 1995
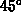 provides the greatest projectile range when the ground is flat. However, this angle does not seem to work as well if the Baron's artillery batteries are forced to fire uphill or downhill. The Baron wants to know what the optimum angle is in these cases.
provides the greatest projectile range when the ground is flat. However, this angle does not seem to work as well if the Baron's artillery batteries are forced to fire uphill or downhill. The Baron wants to know what the optimum angle is in these cases.
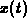 will be the distance that the Baron is interested in at the value of t where
will be the distance that the Baron is interested in at the value of t where 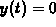 . In setting up your coordinates this way, you introduce two angles,
. In setting up your coordinates this way, you introduce two angles, 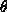 and
and 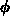 where
where 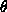 is the angle between the cannon and the ground and
is the angle between the cannon and the ground and 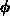 is the angle the ground makes with the horizontal.
is the angle the ground makes with the horizontal.



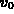 is the initial velocity of the projectile.
is the initial velocity of the projectile.
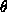 that gives the maximum range for each value of
that gives the maximum range for each value of 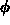 . In writing your report, the following points must be addressed.
. In writing your report, the following points must be addressed.
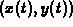 . Note that the variables
. Note that the variables 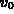 ,
, 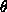 , and
, and 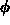 will appear as parameters in your solution.
will appear as parameters in your solution.
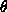 that gives maximum range for a given angle
that gives maximum range for a given angle 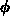 . A plot of
. A plot of 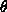 versus
versus 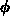 should be provided for the use of the Baron's field officers.
should be provided for the use of the Baron's field officers.