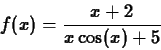Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to explore the geometric and
algebraic aspects of the derivative.
The derivative of a function 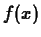 at a point
at a point 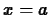 , often written
, often written
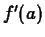 , can be interpreted in several different ways.
, can be interpreted in several different ways.
- Algebraically as the following limit
- Geometrically as the slope of the tangent line to the graph of
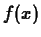 at
at 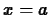 .
.
- Functionally as the instantaneous rate of change of
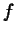 at
at
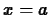 .
.
Probably the second and third interpretations are the most important;
they are certainly closer to what makes the derivative useful. In this
lab, we will use Maple to explore each of these different aspects of
the derivative.
You can use the definition and the Maple limit command to
compute derivatives from the definition, as shown below.
> f := x -> x^2+3*x+5;
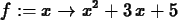
> (f(1+h)-f(1))/h;
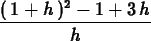
The following limit determines 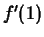 .
.
> limit ((f(1+h)-f(1))/h,h=0);
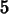
The following limit determines 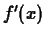 .
.
> limit((f(x+h)-f(x))/h,h=0);
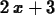
Maple also knows how to compute the
derivatives of most functions. The main command for differentiating
functions is D, also shown in the examples below. The last
example shows how to use the D command to define a function
df that is the derivative of f.
>
D(f);
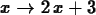
> D(f)(1);
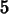
> df := D(f);
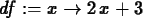
> df(x);
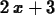
There is also a diff command for differentiating
expresssions. Some examples are given below.
> diff(cos(x),x);
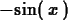
> p := x^3+sin(x);
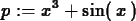
> diff(p,x);
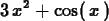
> f(x);
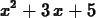
> diff(f(x),x);
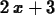
> subs(x=1,diff(f(x),x));
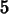
To learn more about how to use the D and diff commands,
see the help pages. In general, the D command is useful for
computing the derivative of a function at a point because it produces
a function. The output of the diff command, on the other
hand, is an expression. Expressions are easy to plot, but putting in
numbers to evaluate an expression requires the subs command,
as shown in the last command in the examples above.
Note the diff command is also available via the
context-sensitive menu for an expression. Just select the
Differentiate item from the menu. However, the menu route
will not work directly on functions and can not be used to obtain the
D command.
The secant line with base point 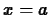 and increment
and increment 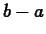 of a function
of a function
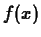 is the straight line passing through the two points
is the straight line passing through the two points 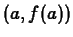 and
and 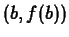 . Given this information, it isn't too hard to write
down the equation for the secant line, given a function, base point,
and increment as
. Given this information, it isn't too hard to write
down the equation for the secant line, given a function, base point,
and increment as
However, to save you some trouble, the secantline
function has been written. This function is not a standard part of
Maple, but is one of about thirty Maple commands that have been
written at WPI for calculus. In the examples below, the first command
shows you how to load the CalcP package containing these
commands. You must do this before you
can use secantline. If the output from the with(CalcP);
command is different from what you see below, or the secantline
command doesn't seem to work, ask for help.
The secantline command takes three arguments. The first is a
function or expression, the next one is the base point, and the third
is the increment 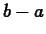 . Try the commands in the examples below to learn how
to use this command. If you want to learn more, consult the help
page. Note especially that the third argument to
secantline is not
. Try the commands in the examples below to learn how
to use this command. If you want to learn more, consult the help
page. Note especially that the third argument to
secantline is not 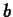 , but
, but 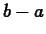 .
.
Also new in the examples is the Maple animate command, which is part of the Maple plots package. You
must issue the with(plots); command before you can use animate.
The animate command first produces what looks like an ordinary
plot in the worksheet. However, if you click on the plot to make it
active, controls for the animation appear in the context bar
that are similar to
those on a VCR. You should be able to figure out how they work by
experimenting. In the examples below, the animate command shows the
tangent line as the limit of secant lines.
> with(CalcP);
![\begin{maplelatex}
\begin{eqnarray*}
\lefteqn{[{\it ArcInt}, {\it Curvature}, {\...
...it tanvect}, {\it unitvect}]\mbox{\hspace{14pt}}
\end{eqnarray*}\end{maplelatex}](img23.gif)
> f := x -> x^3-2*x+1 ;
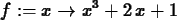
> secantline(f,x=0,1);
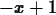
> secantline(f,x=0,0.5);
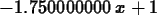
> plot({f(x),secantline(f,x=0,1),secantline(f,x=0,0.5)},x=0..1);
> with(plots):
> animate({f(x),secantline(f,x=0,1.5-t)},x=-0.5..1.5,t=0..1.49);
> secantline(f,x=0,h);
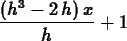
> limit(secantline(f,x=0,h),h=0);
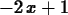
- Find the derivatives of the following functions three different
ways using Maple. From the definition, using the D command, and
using the diff command. Note that Maple has its own ideas of
what form the answer should take, so some of your answers may look
unfamiliar or be more complicated than you think they should.
-
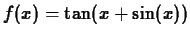
-
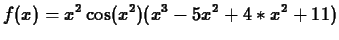
-
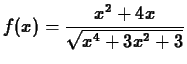
- Given the function
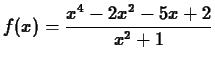 ,
,
- Plot
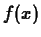 between
between
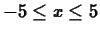 .
.
- Find the slope of the line tangent to the graph at
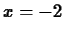 .
.
- Find any other points on the graph of
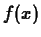 that have the same
slope as the tangent line at
that have the same
slope as the tangent line at 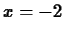 .
.
- For the function given below,
- Find the equation of the line tangent to the graph of
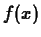 at
the point
at
the point 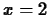 .
.
- Plot the function and the tangent line on the same graph.
- Find a point on the graph for which the tangent line is
perpendicular to the tangent line at
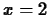 . You need only consider
. You need only consider
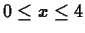 .
.
- In the case that
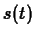 is the position of an object as a
function of time, the difference quotient
is the position of an object as a
function of time, the difference quotient
can be interpreted as the average velocity of the object during the
time interval ![$[a,b]$](img40.gif) and the limit of the difference quotient is the
instantaneous velocity. Suppose that the position in meters of an object is
given by
and the limit of the difference quotient is the
instantaneous velocity. Suppose that the position in meters of an object is
given by
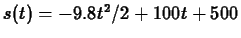 where
where 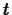 is time in seconds.
is time in seconds.
- What is the average velocity of the object over the interval
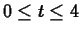 ? Include a plot of
? Include a plot of 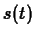 and an appropriate secant
line whose slope is equal to this average velocity.
and an appropriate secant
line whose slope is equal to this average velocity.
- What is the average velocity over the time interval
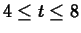 ?
?
- Is there a time between
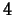 and
and 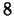 at which the instantaneous
velocity is equal to the average velocity over the time interval
at which the instantaneous
velocity is equal to the average velocity over the time interval
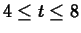 ?
?
- At what time is the instantaneous velocity equal to
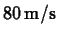 ?
?
- At what time is the instantaneous velocity equal to zero?



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2000-09-26
![]() .
.
![]() .
.
![]() . Try the commands in the examples below to learn how
to use this command. If you want to learn more, consult the help
page. Note especially that the third argument to
secantline is not
. Try the commands in the examples below to learn how
to use this command. If you want to learn more, consult the help
page. Note especially that the third argument to
secantline is not ![]() , but
, but ![]() .
.
![\begin{maplelatex}
\begin{eqnarray*}
\lefteqn{[{\it ArcInt}, {\it Curvature}, {\...
...it tanvect}, {\it unitvect}]\mbox{\hspace{14pt}}
\end{eqnarray*}\end{maplelatex}](img23.gif)
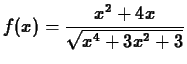
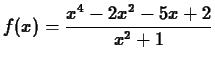 ,
,