Subsections

• Exercises

Limits of functions.

Limits of many functions and expressions can be computed in Maple with the limit command.

  > limit(sin(x)/x,x=0);

  > g := x -> (3*x^2+4)/(x^2+7*x+12) ;

  > limit(g(x),x=-2);

  > limit(g(x),x=-4);

If the limit exists, Maple can usually find it. In cases where the limit doesn't exist, Maple gives the answer $\infty, -\infty$ or undefined for an unbounded limit. In the case that the limit doesn't exist because the function oscillates, Maple gives a range such as -1..1 if the limit doesn't exist.

  > limit(1/x,x=0);

  > limit(1/x^2,x=0);

  >  limit(sin(1/x),x=0);

Maple can also do one-sided limits. Use Maple's online help to find out how to handle such limits.

Note that there is a Limit item on the Constructions submenu of the context sensitive menu for a Maple expression. Using this item will produce a Limit command. This is different from the limit command described above and is an example of what is called an inert command in Maple. In the case of the Limit command, all it does is display the mathematical notation for the limit without attempting to evaluate it. The usual way to get Maple to evaluate an inert command (like Limit) is to use the value command. However, it is almost always simpler to use the limit command and that is what you are encouraged to do for this lab.

The following definition of limit is given on page 66 of the text.

Definition 1   To say that $$\lim_{x\rightarrow c} f(x) = L$$ means that for each $\epsilon > 0$ (no matter how small), there is a corresponding $\delta > 0$ such that $\mid f(x) - L\mid < \epsilon$ provided that $0 < \mid x - c \mid < \delta$; that is

$$0 < \mid x - c \mid < \delta \, \Rightarrow \, \mid f(x) - L\mid < \epsilon$$

This definition may seem complicated, but it has a nice graphical interpretation. Plot $f$ with the $y$-range set to $(L-\epsilon, L+\epsilon)$ and the $x$-range set to $(c-\delta, c+\delta)$. Try to choose $\delta$ small enough so that the graph of $f$ stays between the top and bottom of the plot. If you can find such a $\delta$ no matter how small the $\epsilon$, then the limit exists and is equal to $L$.

Consider this example. Let $f(x) = x^2,\;\;c = 2$ and $\epsilon = 0.2$. Then any value for $\delta$ smaller than about $0.049$ will work. To see why this is so look at the plots generated by the following commands.

  > f:=x->x^2;

  > limit(f(x), x = 2);

  > plot({4-0.2,4+0.2,f(x)},x=2-0.1..2+0.1,y=4-0.2..4+0.2);

  > plot({4-0.2,4+0.2,f(x)},x=2-0.048..2+0.048,y=4-0.2..4+0.2);

In the first of the two plot commands, the value of $\delta$ is $0.1$. This is too large since the graph intersects the lines $y = 4 - 0.2$ and $y = 4 + 0.2$. The $0.048$ value for $\delta$ in the second plot command, however, is small enough since the graph of $f$ goes out the sides of the plot. Make sure you understand what is done in this example since you will need to do similar work in some of the exercises. You may find that using the smartplot command is convenient to use, because you can easily edit the plot ranges. On the other hand, smart plots take longer to appear. The choice is yours.

Exercises

In Exercises 1 and 2, use the limit command to find $$\lim_{x \rightarrow c}f(x)$$. Then experiment with some plots to find a $\delta$ that works for $\epsilon = 0.1.$ Also, find a $\delta$ that doesn't work. These two $\delta$ values should be close to each other. Thus your $\delta$ that works should be near the largest value of $\delta$ that can be used. Although, you will probably need to do many plots, submit only the two required plots with your worksheet. These plots should be in the style of the example above. Next, repeat the problem with $\epsilon = 0.01$. Conclude with a one paragraph statement of what you have learned in the exercise.

1. $s(x) = \displaystyle\frac{x^3 - 12x^2 + 5 x - 1}{x^3 + 4x^2 + 3x - 5}, \;\;c = -2$
2. $w(x) = \displaystyle\frac{x-\sin(2x)}{\tan(x)},\;\;c = 0$
3. Consider the following limit statement
   
   $$\lim_{x \rightarrow \infty} \frac{x+5}{\sqrt{4x^2+2x}} = \frac{1}{2}$$
   
   
   The rigorous definition of a limit in this case says that $$\lim_{x \rightarrow \infty} f(x) = L$$ if for each $\epsilon > 0$ there is a corresponding number $M$ such that
   
   $$x > M \, \Rightarrow \, \mid f(x) - L\mid < \epsilon$$
   
   
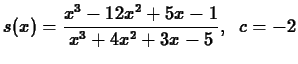
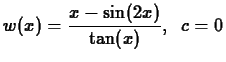
   First, use the limit command to find the limit. Then, given $\epsilon = 0.01$ find a value of $M$ that works in the definition. Try to find the smallest such $M$. Note that Maple uses the word infinity for $\infty$ and that infinity can be used in the limit command and in a range for the plot command, e.g. x=2..infinity.

4. Consider the following limit.

   
   

   $$\lim_{x \rightarrow 0} x \sin(1/x)$$
   
   
   Use Maple to compute this limit. Then explain why this does not imply the existence of the following limit.
   
   $$\lim_{x \rightarrow 0} \sin(1/x)$$