


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to teach you how to use Maple commands for
computing derivatives.
You can compute derivatives in Maple using the limit definition of the derivative and Maple's limit command. The more common methods of computing derivative in Maple are the diff command for differentiating expressions and
the D operator for differentiating functions. We will compute derivatives using all three methods.
Using the definition of derivative
,
you can do this in Maple by first defining the difference quotient and the computing the limit. The following example shows how to compute the derivative of 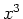 and the evaluate the derivative at
and the evaluate the derivative at 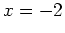 .
.
> f:=x-> x^3;
> quot := (f(x+h)-f(x))/h;
> der:=limit(quot,h=0);
> subs(x=-2,der);
or if you don't need to see that the derivative of 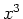 is
is 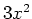 and you just want to evaluate the derivative at
and you just want to evaluate the derivative at 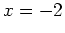 , then this could be done all in one Maple command as in the following example:
, then this could be done all in one Maple command as in the following example:
> f:=x->x^3;
> limit((f(-2+h)-f(-2))/h,h=0));
These commands can be summarized as follows.
- The D
operator acts on a function to produce the derivative of that
function.
- The diff command acts on an expression and
differentiates that expression with respect to a variable specified by
the user.
When you use the D operator to compute the derivative of a
function, the result is also a function, as shown below.
> D(f);
If you provide a label, then you get a function you can use later in
the session,
> df := D(f);
However, this is usually not necessary. See the examples below.
If you want to evaluate the derivative at a specific value of 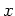 or
just get the expression for the derivative, you can use the following
forms of the D operator.
or
just get the expression for the derivative, you can use the following
forms of the D operator.
> D(f)(2);
> D(f)(x);
This last form is the one to use for plotting, as shown below.
> plot(D(f)(x),x=-2..2);
Suppose you want to find the equaton of the line tangent to the graph of 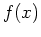 at the point
at the point 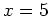 . This can be done in Maple using the point slope form of a line as shown below.
. This can be done in Maple using the point slope form of a line as shown below.
> tanline := D(f)(5)*(x-5)+f(5);
The D operator cannot be used on expressions, for example
trying to use it to differentiate the expresssion we defined above
results in an error.
> D(p);
If you recall that Maple uses f(x) to refer to the
expresssion that is used to define 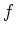 , then the following error
shouldn't surprise you.
, then the following error
shouldn't surprise you.
> D(f(x));
To differentiate expressions, you need to use the diff
command. Here is an example.
> diff(p,x);
The diff command can also be applied to functions as shown
below.
> diff(f(x),x);
Note, however, that the result of the diff command is an
expression, not a function. This means that computing the value of the
derivative at a specific value of 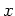 requires you to use the
subs command as follows:
requires you to use the
subs command as follows:
> der := diff(p,x);
> subs(x=Pi/2,der);
- Show that the derivative of the function
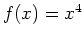 is
is 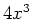 by using the limit definition of derivative.
by using the limit definition of derivative.
- Use a variable name and expression notation to define
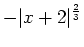 ,
,
- Compute the derivative and label the derivative using a variable name.
- Evaluate the derivative at
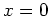 ,
, 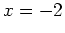 , and
, and 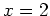 .
.
- Plot the expression over the interval
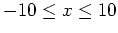 . Using this plot, can you explain why the expression was not differentiable at one of the
. Using this plot, can you explain why the expression was not differentiable at one of the 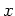 values given above?
values given above?
- Find the equation of the line tangent to the graph of the function
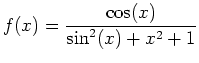 at
at 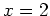 . When calculating the derivative at a point, use the
. When calculating the derivative at a point, use the 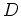 command. Include a plot of the function and the tangent line on the same graph over the interval
command. Include a plot of the function and the tangent line on the same graph over the interval
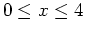 .
.
- For the same function,
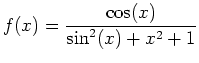 ,
,
- Plot
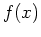 over the interval
over the interval
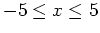 and state how many horizontal tangent lines to the graph there are ONLY in this interval.
and state how many horizontal tangent lines to the graph there are ONLY in this interval.
- Plot the derivative of
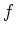 over the same interval. Explain how this supports your answer above.
over the same interval. Explain how this supports your answer above.
- Using the fsolve command along with labels, find each
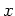 value where a horizontal tangent line is located. Find the corresponding
value where a horizontal tangent line is located. Find the corresponding 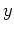 values by plugging each
values by plugging each 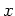 value back into the function. State in text all points on the graph of
value back into the function. State in text all points on the graph of 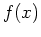 where the tangent line is horizontal.
where the tangent line is horizontal.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2008-09-17
![]() or
just get the expression for the derivative, you can use the following
forms of the D operator.
or
just get the expression for the derivative, you can use the following
forms of the D operator.
![]() at the point
at the point ![]() . This can be done in Maple using the point slope form of a line as shown below.
. This can be done in Maple using the point slope form of a line as shown below.
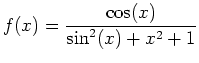 at
at 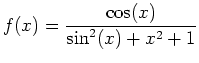 ,
,