Subsections

• Simple limits and Maple
• Derivatives
  • The limit definition of the derivative
  • The Maple D and diff commands
  
  
• Exercises

Limits of Functions.

Simple limits and Maple

Limits of many functions and expressions can be computed in Maple with the limit command. Some examples are given below.

> limit(x^2+2*x,x=2);
> limit(sin(x)/x,x=0);
> f := x -> (x+3)/(x^2+7*x+12);
> limit(f(x),x=-3);
> limit(f(x),x=-4);

If the limit exists, Maple can usually find it. In cases where the limit doesn't exist, Maple gives the answer undefined or sometimes infinity for an unbounded limit or gives a range like -1..1 if the limit doesn't exist, but the expression or function is bounded.

You can also calculate one sided limits in Maple as shown in the example below.

> g:=x->(x-2)/(x^2-4)
> g(2);
> limit(g(x),x=2,left);
> limit(g(x),x=2,right);
> limit(g(x),x=2);

Derivatives

You can compute derivatives in Maple using the limit definition of the derivative and Maple's limit command. The more common methods of computing derivative in Maple are the diff command for differentiating expressions and the D operator for differentiating functions. We will compute derivatives using all three methods.

The limit definition of the derivative

Using the definition of derivative

$$\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$$

, you can do this in Maple by first defining the difference quotient and the computing the limit. The following example shows how to compute the derivative of $x^3$ and the evaluate the derivative at $x=-2$.

> f:=x-> x^3;
> quot := (f(x+h)-f(x))/h;
> der:=limit(quot,h=0);
> subs(x=-2,der);

or if you don't need to see that the derivative of $x^3$ is $3x^2$ and you just want to evaluate the derivative at $x=-2$, then this could be done all in one Maple command as in the following example:

> limit((f(-2+h)-f(-2))/h,h=0);

The Maple D and diff commands

These commands can be summarized as follows.

• The D operator acts on a function to produce the derivative of that function.
• The diff command acts on an expression and differentiates that expression with respect to a variable specified by the user.

When you use the D operator to compute the derivative of a function, the result is also a function, as shown below.

> D(f);

If you provide a label, then you get a function you can use later in the session,

> df := D(f);

However, this is usually not necessary. See the examples below.

If you want to evaluate the derivative at a specific value of $x$ or just get the expression for the derivative, you can use the following forms of the D operator.

> D(f)(2);
> D(f)(x);

This last form is the one to use for plotting, as shown below.

> plot(D(f)(x),x=-10..10);

The D operator cannot be used on expressions, for example trying to use it to differentiate the expresssion we defined above results in an error.

> D(p);

If you recall that Maple uses f(x) to refer to the expresssion that is used to define $f$, then the following error shouldn't surprise you.

> D(f(x));

To differentiate expressions, you need to use the diff command. Here is an example.

> diff(p,x);

The diff command can also be applied to functions as shown below.

> diff(f(x),x);

Note, however, that the result of the diff command is an expression, not a function. This means that computing the value of the derivative at a specific value of $x$ requires you to use the subs command as follows:

> der := diff(p,x);
> subs(x=Pi/2,der);

Suppose you want to find where the tangent line to the graph of $f(x)$ is horizontal. This can be done first by plotting the derivative to see how many times the graph crosses the $x$-axis, then using Maple's solve or fsolve commands as shown below.

> f:=x->x^4-16*x^2+x/4;
> plot(D(f)(x),x=-5..5);
> solve(D(f)(x)=0,x)
> fsolve(D(f)(x)=0,x)

Exercises

1. Calculate the left and right hand limits for each function below as $x$ approaches $-3$ and state whether or not the function is continuous at the point $x=-3$ and why.
   1. 
      
      $$f(x) = \frac{x+3}{\vert x^2+7x+12\vert}$$
      
      

   2. 
      
      $$f(x) = \frac{x+3}{x^2+7x+12}$$
      
      

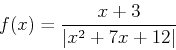
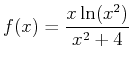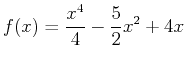2. Find the dervative of the function $$f(x)=\frac{x\ln(x^2)}{x^2+4}$$ using the limit definition of the derivative, the diff command and then the D command and then use all three methods to find the slope of $f$ at $x=-1$.
3. For the function $$f(x)=\frac{x^4}{4}-\frac{5}{2}x^2+4x$$,
   1. Plot $f(x)$ over the interval $-5 \leq x \leq 5$ and state how many horizontal tangent lines to the graph that you think there are.
   2. Plot the derivative of $f$. Explain how this supports your answer above. You may need to adjust your plotting range.
   3. Using the fsolve command along with labels, find each $x$ value where a horizontal tangent line is located. Find the corresponding $y$ values by plugging each $x$ value back into the function. State in text all points on the graph of $f(x)$ where the tangent line is horizontal.