


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
To find critical points you use the first derivative to find where the slope is zero or undefined.
> f:=x->x^3-3*x+1;
> plot(f(x),x=-3..3);
> solve(D(f)(x)=0,x);
Where the function has a denominator remember to check where the derivative is undefine as well as zero.
> g:=x->x^4/(7*x+5);
> plot(g(x),x=-3..3,y=-3..3);
> solve(D(g)(x)=0,x);
> solve(D(g)(x)=infinity);
The above command doesn't work so enter the denominator (using the denom command to single out the denominator) or reciprocal equal to zero. That is the same as the equation equal to infinity.
> solve(denom((D(g))(x)) = 0, x);
> solve(1/D(g)(x)=0,x);
So, the function 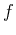 has two critical values and the function
has two critical values and the function 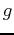 has three critical values.
To check for maximum and minimum values using the first-derivative test, check the INTERVALS between the critival values. Using
has three critical values.
To check for maximum and minimum values using the first-derivative test, check the INTERVALS between the critival values. Using 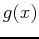 as our example, we know there are three critical values therefore there are four intervals that need to be checked. You want to know if the function is going uphill or downhill on the interval so you must plug into the slope which is the FIRST derivative.
as our example, we know there are three critical values therefore there are four intervals that need to be checked. You want to know if the function is going uphill or downhill on the interval so you must plug into the slope which is the FIRST derivative.
> D(g)(-5); D(g)(-6/7); D(g)(-1/2); D(g)(5);
It is only the positive or negative sign that is important. The function increases on the interval
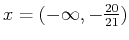 , then decreases on the interval
, then decreases on the interval
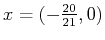 , and finally increases on the interval
, and finally increases on the interval
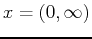 . Therefore, there is a maximum at
. Therefore, there is a maximum at
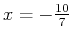 and a minimum at
and a minimum at 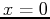 .
To find the same maximum and minimum values using the second-derivative test simply plug the critical points into the SECOND derivative to check concavity. (Do not use interval values.)
.
To find the same maximum and minimum values using the second-derivative test simply plug the critical points into the SECOND derivative to check concavity. (Do not use interval values.)
> D[1,1](g)(-20/21); D[1,1](g)(-5/7); D[1,1](g)(0);
(Note the [1,1] is the syntax for the second derivative NOT the point)
Only
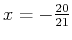 and
and 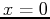 have concavity. Therefore, there is a maximum at
have concavity. Therefore, there is a maximum at
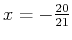 and a minimum at
and a minimum at 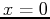 .
Absolute extrema is the easiest because all that is important is what is the highest and lowest
.
Absolute extrema is the easiest because all that is important is what is the highest and lowest 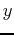 value. The surrounding slope and concavity are not important. Therefore all you need to do is check the y-values. Using
value. The surrounding slope and concavity are not important. Therefore all you need to do is check the y-values. Using 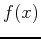 as our example, this time the question will be what is the ABSOLUTE extrema of
as our example, this time the question will be what is the ABSOLUTE extrema of 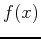 on the interval
on the interval
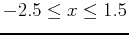 .
Using the critical points:
.
Using the critical points:
> solve(D(f)(x)=0,x);
and the two endpoints 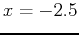 and
and 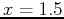 .Simply find the four y values and pick the highest and lowest value.
.Simply find the four y values and pick the highest and lowest value.
> f(-2.5); f(-1); f(1); f(1.5);
Therefore, the ABSOLUTE extrema are (-2.5, -7.13) and (-1, 3).
- For the function
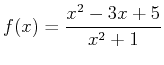
- A)
- Find ALL critical values and state them in text.
- B)
- Use the first derivative test to find intervals on which
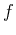 is increasing and intervals on which it is decreasing without looking at a plot of the function.
is increasing and intervals on which it is decreasing without looking at a plot of the function.
- Without plotting the function
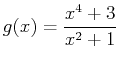 , find all critical points and then classify each point as a relative maximum or a relative minimum using the second derivative test. Be sure to find corresponding
, find all critical points and then classify each point as a relative maximum or a relative minimum using the second derivative test. Be sure to find corresponding 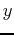 values for each critical value. (You do not need to consider where the derivative is undefined here because there could never be a relative extrema at a point where
values for each critical value. (You do not need to consider where the derivative is undefined here because there could never be a relative extrema at a point where 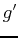 is undefined.)
is undefined.)
- Find the absolute extrema for the function
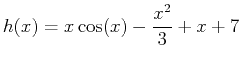 on the closed interval
on the closed interval ![$[1,7]$](img19.png) without plotting the function. Plot the derivative of the function and use fsolve to help you find critical values.
without plotting the function. Plot the derivative of the function and use fsolve to help you find critical values.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2017-09-26
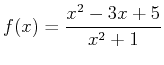
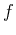 is increasing and intervals on which it is decreasing without looking at a plot of the function.
is increasing and intervals on which it is decreasing without looking at a plot of the function.
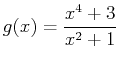 , find all critical points and then classify each point as a relative maximum or a relative minimum using the second derivative test. Be sure to find corresponding
, find all critical points and then classify each point as a relative maximum or a relative minimum using the second derivative test. Be sure to find corresponding 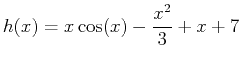 on the closed interval
on the closed interval