Limits of many functions and expressions can be computed in Maple with the limit command. Some examples are given below.
> limit(x^2+2*x,x=2);
> limit(sin(x)/x,x=0);
> f := x -> (x+3)/(x^2+7*x+12) ;
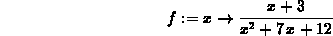
> limit(f(x),x=-3);
> limit(f(x),x=-4);
If the limit exists, Maple can usually
find it. In cases where the limit doesn't exist, Maple gives the
answer infinity for an unbounded limit or gives a range like
-1..1 if the limit doesn't exist, but the expression or
function is bounded. See the examples below.
> limit(1/x,x=0);
> limit(sin(1/x),x=0);
You can also use Maple to compute limits as x goes to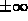 
as shown below.
> f(x);
> limit(f(x),x=infinity);
> limit(f(x),x= -infinity);
The formal definition for a limit is given below.
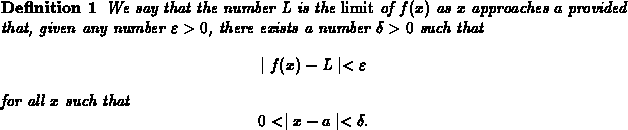
This definition may seem
complicated, but its graphical interpretation is not so bad. It says
that if you plot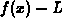 
with the y range set to
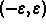you can always choose a value of 
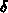small enough so that when you shrink the x plot range to
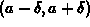and plot the function, its graph will not
intersect the top or the bottom edges of your plot. For example,
suppose 
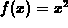, a=2 and 
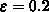. Then any value of
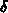smaller than about 
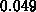will work. To see what is going
on, look at the plots generated by the following commands.
> f := x -> x^2;
> limit(f(x),x=2);
> plot({-0.2,0.2,f(x)-4},x=2-0.1..2+0.1,y=-0.2..0.2);
> plot({-0.2,0.2,f(x)-4},x=2-0.048..2+0.048,y=-0.2..0.2);
In the first of the two plot commands, the value of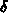 
is
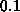. This is too large, since the graph intersects the lines
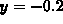and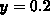 
. The value of 
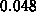for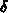 
in the second
plot command, however, is small enough, since the graph of
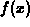goes off the sides of the plot. Make sure that you understand
this example. If you don't understand, ask for help.