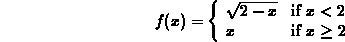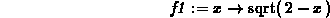Next: Exercises
Up: Background
Previous: Simple limits and
It should be no secret by now that for most
functions 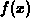 defined by a single formula,
defined by a single formula, 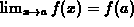 when
when 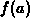 exists. For more complicated functions, this
may not be true. For dealing with some of these exceptional cases, we
need to define right-hand and left-hand limits. Loosely speaking, the
right-hand limit of
exists. For more complicated functions, this
may not be true. For dealing with some of these exceptional cases, we
need to define right-hand and left-hand limits. Loosely speaking, the
right-hand limit of 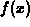 at a is L if
at a is L if 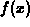 approaches L as
x approaches a from the right. That is, the values of x satisfy
x > a. The left-hand limit is defined in an analogous manner, with
the values of x approaching a from the left. Maple can
compute these special limits with commands like those shown below. The
Maple floor function is actually the greatest integer function.
approaches L as
x approaches a from the right. That is, the values of x satisfy
x > a. The left-hand limit is defined in an analogous manner, with
the values of x approaching a from the left. Maple can
compute these special limits with commands like those shown below. The
Maple floor function is actually the greatest integer function.
> plot(floor(x),x=0..4);
> limit(floor(x),x=1,right);

> limit(floor(x),x=1,left);

The floor function is one of Maple's defined functions, so you
might expect things to work properly. If you define your own function
in a piecewise fashion, however, a different approach is needed.
For example, suppose you wanted to find the limit as x approaches
2 for the following function:
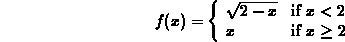
You would need to execute the following commands:
> f1 := x -> sqrt(2-x);
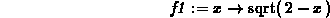
> limit(f1(x),x=2,left);

> f2 := x -> x;

> limit(f2(x),x=2,right);

From this, we see that the limit of f as x approaches 2 does not exist since the limit from the left does not equal the limit from the right.
William W. Farr
Thu Sep 7 15:27:05 EDT 1995
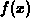 defined by a single formula,
defined by a single formula, 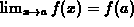 when
when 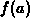 exists. For more complicated functions, this
may not be true. For dealing with some of these exceptional cases, we
need to define right-hand and left-hand limits. Loosely speaking, the
right-hand limit of
exists. For more complicated functions, this
may not be true. For dealing with some of these exceptional cases, we
need to define right-hand and left-hand limits. Loosely speaking, the
right-hand limit of 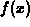 at a is L if
at a is L if 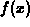 approaches L as
x approaches a from the right. That is, the values of x satisfy
x > a. The left-hand limit is defined in an analogous manner, with
the values of x approaching a from the left. Maple can
compute these special limits with commands like those shown below. The
Maple floor function is actually the greatest integer function.
approaches L as
x approaches a from the right. That is, the values of x satisfy
x > a. The left-hand limit is defined in an analogous manner, with
the values of x approaching a from the left. Maple can
compute these special limits with commands like those shown below. The
Maple floor function is actually the greatest integer function.