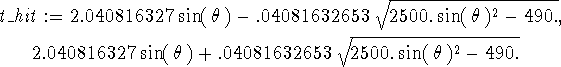
For this part of the lab, load the worksheet
/usr7/bfarr/Maple/solve.mswhich contains one of the partial solutions to the problem from the previous lab. Go through the worksheet and execute all of the commands, ending with the plot. Notice that the command for finding the time t_hit has been changed so that we are finding the time when y=5. This command and the output you should get are shown below. If you get something different, you may want to ask for help.
> t_hit := solve(y(t) = 5,t);
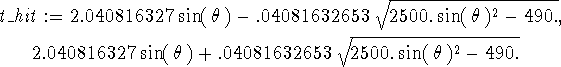
Next, type in the the following command on the first blank input
line. The notation t_hit[2] is used to select the second
solution for t_hit from the two shown above.
> solve(x(t_hit[2]) = 30,theta);
This first method has given us the two solutions we could see in the plot. We could call this first method a sequential method, because we first solved the equation for y and then the equation for x. An alternative method that requires less typing is to solve the two equations simultaneously with the following command.
> solve({x(t) = 30, y(t) = 5},{t,theta});
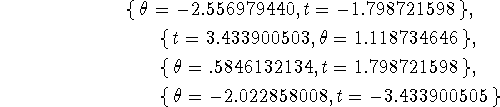
The first argument to the solve command always consists of the equation(s) to be solved. When you want to solve two or more equations simultaneously, you have to enclose them in curly braces, {}. Otherwise, Maple would have trouble figuring out how many equations there are. The second argument to the solve command is the variable(s) to solve for. The general rule is that you need as many variables to solve for as you have equations. If you don't specify the correct number of variables to be solved for, then Maple probably won't be able to solve the equations. As was done for the equations, you must enclose the variables to be solved for inside curly braces.
Maple uses curly braces to denote a set. In a set, order isn't
important so your output may have the solutions reported in a
different order. The way Maple orders the items when printing out a
set is done by memory location, so it doesn't always make sense. For
example, three of the solutions reported above give 
first and
t second, but one has the order reversed.
Solving the two equations simultaneously gives us the two solutions we had before, but it also gives us two solutions we didn't have before. It often happens that Maple gives you several solutions and you must decide which (if any) are the ones you want. In the present case, this is easy because the two unwanted solutions have negative values of t and are not physically important. In fact the two unwanted solutions come from the first value of t_hit, which we ignored in the the sequential solution.
When the solve command is given a set of equations and a set of variables to solve for, the result of the solve command is one or more solution sets. To pick out one of the sets, we can use the trick we used previously of labeling the solve command and using subscripts as shown below.
> sol1 := solve({x(t) = 30, y(t) = 5},{t,theta});
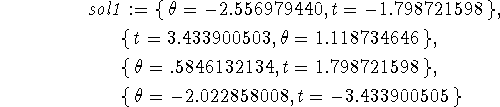
> sol1[2];
Note that if you got the solutions in a different order than shown here, you may need to use an index other than 2 to extract the solution you want.
If you need one of the values from a solution set, the easiest way to
extract it is with the following trick, using the subs
command. The trick is to substitute into an expression consisting
simply of the variable whose value is desired. For example, we can get
the value of from the second solution set with the following command.
> subs(sol1[2],theta);
Solving the two equations simultaneously takes less typing, but we did
lose some information and flexibility. When we solved the equations
seqentially we were able to identify and reject the non-physical
solution and, more importantly, plot the distance as a function of
. The plot provides a lot of information, including the
following points.
value of about 0.84.