Next: About this document ... Up: No Title Previous: No Title
![]()
![]()
![]()
Next: About this document ...
Up: No Title
Previous: No Title
![]()
You can use the definition and the Maple limit command to compute derivatives from the definition, as shown below.
> f := x -> x^2+3*x+5;
> (f(1+h)-f(1))/h;
The following limit determines f'(1).
> limit ((f(1+h)-f(1))/h,h=0);
The following limit determines f'(x).
> limit((f(x+h)-f(x))/h,h=0);
Maple also knows how to compute the derivatives of most functions. The main command for differentiating functions is D, also shown in the examples below. The last example shows how to use the D command to define a function df that is the derivative of f.
> D(f);
> D(f)(1);
> df := D(f);
> df(x);
There is also a diff command for differentiating expresssions. Some examples are given below.
> diff(cos(x),x);
> p := x^3+sin(x);
> diff(p,x);
> f(x);
> diff(f(x),x);
> subs(x=1,diff(f(x),x));
To learn more about how to use the D and diff commands, see the help pages. In general, the D command is useful for computing the derivative of a function at a point because it produces a function. The output of the diff command, on the other hand, is an expression. Expressions are easy to plot, but putting in numbers to evaluate an expression requires the subs command, as shown in the last command in the examples above.
The secant line with base point x=a and increment b-a of a function f(x) is the straight line passing through the two points (a,f(a)) and (b,f(b)). Given this information, it isn't too hard to write down the equation for the secant line, given a function, base point, and increment as
![]()
The secantline command takes three arguments. The first is a function or expression, the next one is the base point, and the third is the increment b-a. Try the commands in the examples below to learn how to use this command. If you want to learn more, consult the help page.Note especially that the third argument to secantline is not b, but b-a.
Also new in the examples is the Maple animate command, which is part of the Maple plots package. You must issue the with(plots); command before you can use animate. The animate command first produces what looks like an ordinary plot in the worksheet. However, if you click on the plot to make it active, controls for the animation appear in the context bar that are similar to those on a VCR. You should be able to figure out how they work by experimenting. In the examples below, the animate command shows the tangent line as the limit of secant lines.
> with(CalcP);
![\begin{maplelatex}
\begin{eqnarray*}
\lefteqn{[{\it ArcInt}, {\it Curvature}, {\...
...\it tanvect}, {\it unitvect}]\mbox{\hspace{14pt}}\end{eqnarray*}\end{maplelatex}](img13.gif)
> f := x -> x^3-2*x+1 ;
> secantline(f,x=0,1);
> secantline(f,x=0,0.5);
> plot({f(x),secantline(f,x=0,1),secantline(f,x=0,0.5)},x=0..1);
> with(plots):
> animate({f(x),secantline(f,x=0,1.5-t)},x=-0.5..1.5,t=0..1.49);
> secantline(f,x=0,h);
> limit(secantline(f,x=0,h),h=0);
![]()
![]()
![]()
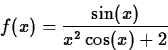
![]()
Dina Solitro