> f:=x->x^2+7*x+5; > g:=x^3-5*x+8;Here are some examples that show how D and diff work. Check the difference between these two commands.
> D(f)(x); > diff(g,x); > diff(f(x),x);See what happens when the function or expression notations are used incorrectly.
> diff(g(x),x); > diff(f,x);After the last four examples, you should be convinced that proper notation is very important in doing derivatives in Maple. Maple can also do higher derivatives. Check these commands. Again, pay attention to the difference between expressions and functions.
> diff(g,x,x); > diff(g,x,x,x); > (D@@2)(f)(x); > (D@@3)(f)(x);If you want to evaluate the higher derivative at a specific value of x, you can use the following
> (D@@2)(f)(2); > subs(x=3,diff(g,x));Suppose you wanted to find the equation of the tangent line to the graph of f(x) at the point x = 5. This can be done in Maple using the point-slope form of a line as shown below. It is not necessary to label the command tanline; but giving the line a name makes it can easy to call it up if it is needed later.
> tanline := D(f)(5)*(x-5)+f(5);More information on D and diff can be obtained through Maple help screens.
> f:=x^2*y^2+y^3=0; > implicitdiff(f,y,x);where f is an equation, y is the dependent variable and x is the independent variable. Thus the command as just stated would compute
> g:=x^2+y^3=1; > implicitdiff(g,y,x);Second derivatives can also be taken with implicitdiff. The following command computes
> implicitdiff(g,y,x,x);Maple also has a command for plotting implicitly defined functions. It is in the package plots which must be called before using the command.
> with(plots): > implicitplot(x^2-y^2=1,x=-3..3,y=-3..3);Suppose you want to find the equation of the line tangent to the graph of
> f:=x^2*y^2+y^3=0;
> m:=subs({x=1,y=-1},implicitdiff(f,y,x));
> tanline := y-(-1)=m*(x-1);
> implicitplot({f,tanline},x=0..2,y=-3..0);
Sometimes you want the value of a derivative, but first have to find the coordinates of the point. More than likely, you will have to use the solve or fsolve command for this. However, to get the fsolve command to give you the solution you want, you often have to specify a range for the variable. Plotting the graph of a relation can be a big help in this task. For instance, if you wanted the slope of ![]() as in the previous example at
as in the previous example at ![]() and
and ![]() is negative, but the
is negative, but the ![]() value is not given, then you would first need to solve for
value is not given, then you would first need to solve for ![]() by substituting the
by substituting the ![]() value into
value into ![]() and then solve for
and then solve for ![]() . See how this is done below.
. See how this is done below.
> f:=x^2*y^2+y^3=0; > solve(subs(x=1,f),y);
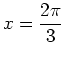 using function notation and
using function notation and
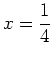 .
.
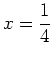 and
and