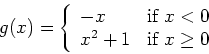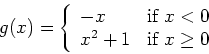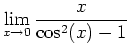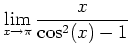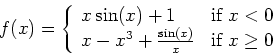Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
Limits of many functions and expressions can be computed in Maple with
the limit command. Some examples are given below.
> limit(x^2+2*x,x=2);
> limit(sin(x)/x,x=0);
> f := x -> (x+3)/(x^2+7*x+12) ;
> limit(f(x),x=-3);
> limit(f(x),x=-4);
If the limit exists, Maple can usually
find it. In cases where the limit doesn't exist, Maple gives the
answer undefined or sometimes infinity for an unbounded
limit or gives a range like
-1..1 if the limit doesn't exist, but the expression or
function is bounded. See the examples below.
> limit(1/x,x=0);
> limit(sin(1/x),x=0);
You can also use Maple to compute limits as 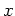 goes to
goes to 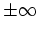 as shown below.
as shown below.
> f(x);
> limit(f(x),x=infinity);
> limit(f(x),x=-infinity);
It should be no secret by now that for most
functions 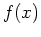 defined by a single formula,
defined by a single formula,
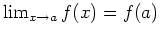 when
when 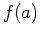 exists. For more complicated functions, this
may not be true.
exists. For more complicated functions, this
may not be true.
If you want to define your own
piecewise-defined function, then the Maple piecewise command
is the best way to do it. Suppose you wanted to define the following
function.
Then the Maple command would be the following.
> g := x -> piecewise(x < 0, -x, x^2+1);
If you want to see your function in a more familiar form, just run a
command like the one below.
> g(x);
The way the piecewise command works is that you give it a
sequence of pairs of conditions and formulas that define your
function. When you want to evaluate your function at a particular
value of 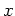 , Maple checks the conditions from left to right until it
finds the one that your value of
, Maple checks the conditions from left to right until it
finds the one that your value of 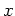 satisifies. It then plugs the
value of
satisifies. It then plugs the
value of 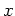 into the next formula. However, notice that the command
above only has one condition and two formulas. This is because any
value of
into the next formula. However, notice that the command
above only has one condition and two formulas. This is because any
value of 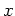 is either less than zero or it is greater than or equal
to zero, so if a particular value of
is either less than zero or it is greater than or equal
to zero, so if a particular value of 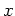 fails the first condition,
i.e. is not less than zero, it must be greater than or equal to zero
and the second formula is the one to use. For more information, see
the help page for piecewise.
fails the first condition,
i.e. is not less than zero, it must be greater than or equal to zero
and the second formula is the one to use. For more information, see
the help page for piecewise.
The limit command works fine for functions that are defined
via the piecewise command, as shown in the example below.
> limit(g(x),x=0);
> limit(g(x),x=0,left);
> limit(g(x),x=0,right);
> plot(g(x), x=-0.1..0.1);
- Use Maple to evaluate each of the limits given below.
-
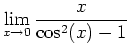
-
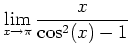
Although both of the above limits do not exist, the output to each Maple command is different. Use a plot to help you explain the difference between the two limits. Be sure that your plotting range for the 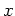 values surround the value that
values surround the value that 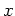 is approaching and you could also limit your
is approaching and you could also limit your  range to
range to ![$[-100,100]$](img10.png) to get a better look at the plots.
to get a better look at the plots.
- Given the following peicewise function:
Plot the function. Does
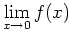 exist? To answer this, you must show that the left and right hand limits agree and are finite. Is the function continuos at
exist? To answer this, you must show that the left and right hand limits agree and are finite. Is the function continuos at 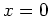 ? Explain your reasoning.
? Explain your reasoning.
- Evaluate the following limit.
Next, write the function as the sum of two fucntions, calculate the limits separately and then explain whether or not the limit of the sum is equal to the sum of the limits. (Hint: You will need to calculate each of the following limits:)



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2007-10-27