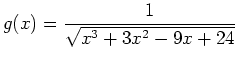Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
Suppose that 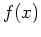 is a differentiable function. Then we
know that the value of
is a differentiable function. Then we
know that the value of 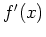 gives the slope of the tangent
line at
gives the slope of the tangent
line at 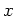 . Geometrically, the slope of the tangent line at a
particular point
. Geometrically, the slope of the tangent line at a
particular point 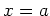 tells us whether the value of the function is
increasing, decreasing, or staying the same as we look at
values of
tells us whether the value of the function is
increasing, decreasing, or staying the same as we look at
values of 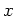 near
near 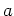 . In applications, one is often trying to find
the minimum or maximum values of a function so it turns out to be
important to be able to determine when a function is increasing and
when it is decreasing. Mathematically, we say that a function is
increasing on an interval
. In applications, one is often trying to find
the minimum or maximum values of a function so it turns out to be
important to be able to determine when a function is increasing and
when it is decreasing. Mathematically, we say that a function is
increasing on an interval  if
if 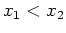 means
means
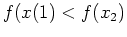 for every pair of numbers
for every pair of numbers 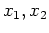 in
in  . Conversely, we we say that
a function is
decreasing on an interval
. Conversely, we we say that
a function is
decreasing on an interval  if
if 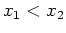 means
means
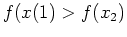 for every pair of numbers
for every pair of numbers 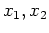 in
in  . These are the definitions
of increasing and decreasing functions, but they are not very easy to
apply. Most often, we use the first derivative as described in the
following theorem.
. These are the definitions
of increasing and decreasing functions, but they are not very easy to
apply. Most often, we use the first derivative as described in the
following theorem.
Theorem 1
Suppose  is continuous on an interval
is continuous on an interval  and differentiable at
every interior point of
and differentiable at
every interior point of  .
.
- If
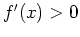 on the interior of
on the interior of  , then
, then  is increasing on
is increasing on
 .
.
- If
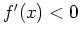 on the interior of
on the interior of  , then
, then  is decreasing on
is decreasing on
 .
.
This theorem says that we can determine when a function is
increasing or decreasing by solving the inequalities 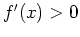 and
and
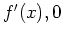 . In practice, we usually work with functions having
continuous derivatives, which means that
. In practice, we usually work with functions having
continuous derivatives, which means that 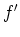 can change sign only at
a point where
can change sign only at
a point where 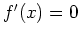 . For example, consider
. For example, consider 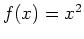 . The
derivative is
. The
derivative is 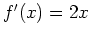 , which is zero only at
, which is zero only at 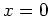 . This critical
point divides the real line up into two intervals,
. This critical
point divides the real line up into two intervals, 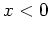 and
and
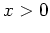 . Since
. Since 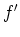 can never be zero if
can never be zero if 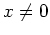 , the sign of
, the sign of 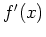 is constant on each interval. That is for
is constant on each interval. That is for 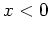 we have
we have 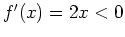 so
so  is decreasing for
is decreasing for 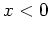 . Similarly,
. Similarly,  is increasing for
is increasing for
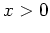 . This suggests the following procedure for determining where a
function is increasing or decreasing.
. This suggests the following procedure for determining where a
function is increasing or decreasing.
- Find the critical points of
 . Note that according to the
definition in the text, critical points of
. Note that according to the
definition in the text, critical points of  are points where either
are points where either
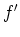 is zero, the derivative doesn't exist, or endpoints of
is zero, the derivative doesn't exist, or endpoints of  if
if  is defined on a finite interval
is defined on a finite interval  .
.
- The critical points divide the domain of
 into subintervals
on which the sign of
into subintervals
on which the sign of 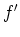 is constant. Check the sign of
is constant. Check the sign of 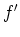 at one
interior point on each subinterval. If it is positive,
at one
interior point on each subinterval. If it is positive,  is
increasing on that subinterval. If it is negative,
is
increasing on that subinterval. If it is negative,  is decreasing
on that subinterval.
is decreasing
on that subinterval.
The second derivative, 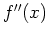 also provides
information about the shape of the curve in terms of what is called
concavity. Concavity can also be defined in several ways. Geometrically,
it can be said that the graph of
also provides
information about the shape of the curve in terms of what is called
concavity. Concavity can also be defined in several ways. Geometrically,
it can be said that the graph of  is concave up near a point
is concave up near a point
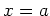 if the tangent line at
if the tangent line at 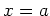 lies below the graph of
lies below the graph of  on some
open interval containing
on some
open interval containing 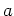 and is concave up if the tangent line
lies above the graph of
and is concave up if the tangent line
lies above the graph of  on some open interval containing
on some open interval containing
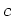 . Algebraically, concavity is most often defined by saying that
. Algebraically, concavity is most often defined by saying that  is concave up on an interval
is concave up on an interval  if
if 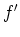 is increasing on
is increasing on  and is
concave down on
and is
concave down on  if
if 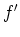 is decreasing on
is decreasing on  . Using the theorem
above and remembering that
. Using the theorem
above and remembering that 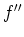 is the derivative of
is the derivative of 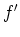 gives the
following result.
gives the
following result.
Theorem 2
Suppose  be twice differentiable on the open interval
be twice differentiable on the open interval  .
.
- If
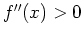 on
on  , then
, then  is concave up on
is concave up on
 .
.
- If
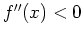 on
on  , then
, then  is concave down on
is concave down on
 .
.
This means that we can find where  is concave up and concave down
using the same procedure on
is concave up and concave down
using the same procedure on 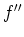 that we used on
that we used on
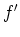 . That is, we first find all of values of
. That is, we first find all of values of 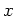 for which
for which 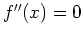 , or
, or
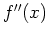 doesn't exist. Including the endpoints, if our domain is a
finite interval, these values of
doesn't exist. Including the endpoints, if our domain is a
finite interval, these values of 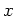 are the endpoints of distinct
subintervals on which the sign of
are the endpoints of distinct
subintervals on which the sign of 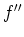 is constant. Checking the sign
of
is constant. Checking the sign
of 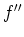 at one point in the interior of each subinterval determines
the concavity of
at one point in the interior of each subinterval determines
the concavity of  on that subinterval.
on that subinterval.
Remember also that the second derivative can be helpful in determining local maximums and local minimums. That is, if you find a critical value, where 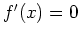 or is undefined, then substitute the critical value into the second derivative. If the second derivative is positive, then there is a relative minimum there and if the second derivative is negative, then there is a relative maximum there.
or is undefined, then substitute the critical value into the second derivative. If the second derivative is positive, then there is a relative minimum there and if the second derivative is negative, then there is a relative maximum there.
The Maple commands that are most useful are the ones for plotting
functions, taking derivatives, and solving equations. By plotting the
function and/or its derivatives, you can get a very good idea of where
it is increasing/decreasing and where it is concave up/concave
down. Then using the solve or fsolve commands
you can find the values of 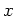 where
where 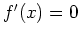 or
or 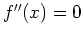 . Finally,
you can use Maple to check the signs of
. Finally,
you can use Maple to check the signs of 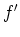 or
or 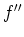 in the interior
of the subintervals. The example below shows how you can use Maple to find intervals where the function
in the interior
of the subintervals. The example below shows how you can use Maple to find intervals where the function
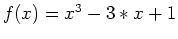 is increasing and decreasing.
is increasing and decreasing.
> f := x-> x^3-3*x+1;
> plot(f(x),x=-3..3);
> solve(D(f)(x)=0,x);
> D(f)(-2);
> D(f)(0);
> D(f)(2);
The plot helps to see how many critical values you have. The solve command shows that there are critical values at 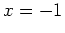 and
and 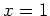 which means that the intervals can be broken up into
which means that the intervals can be broken up into 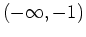 ,
, 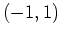 , and
, and 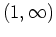 . Remember that if solve doesn't work or doesn't find all critical values, you can use the fsolve command specifying ranges for
. Remember that if solve doesn't work or doesn't find all critical values, you can use the fsolve command specifying ranges for 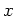 in which to solve. Then chosing a point in each interval, we can see that the value of the derivative is positive at
in which to solve. Then chosing a point in each interval, we can see that the value of the derivative is positive at 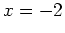 which implies that the function is increasing on the interval
which implies that the function is increasing on the interval 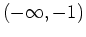 . We can also use the second derivative test to classify
. We can also use the second derivative test to classify 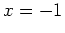 and
and 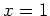 as relative maximum or relative minimum. See the Maple commands below to help you do this.
as relative maximum or relative minimum. See the Maple commands below to help you do this.
> D[1,1](f)(-1);
> f(-1);
> D[1,1](f)(1);
> f(1);
As you can see, the value of the second derivative at 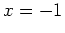 is negative implying that
is negative implying that 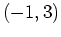 is a relative maximum. The value of the second derivative at
is a relative maximum. The value of the second derivative at 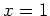 is positive which means that
is positive which means that 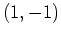 is a relative minimum.
is a relative minimum.
For each exercise below, do NOT look at a plot of the function. You may however, plot the derivative to help you if you need it.
- For the function
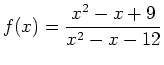 ,
,
- Find all critical values (where the derivative is zero or undefined).
- Find intervals on which
 is increasing and the intervals on which it is decreasing.
is increasing and the intervals on which it is decreasing.
- For the function
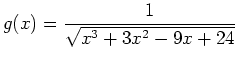
- Find all critical points. (You do not need to consider where the derivative is undefined here because there could never be a relative extrema at a point where
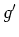 is undefined. Also remember a critical point implies finding corresponding
is undefined. Also remember a critical point implies finding corresponding 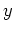 values for each critical value.)
values for each critical value.)
- Use the second derivative test to classify each point as a relative maximum or a relative minimum, again, without plotting the function.
- Find the absolute extrema for the function
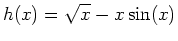 on the closed interval
on the closed interval ![$[0,7]$](img44.png) , again, without plotting the function.
, again, without plotting the function.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2007-11-28
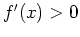 on the interior of
on the interior of  , then
, then  is increasing on
is increasing on
 .
.
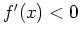 on the interior of
on the interior of  , then
, then  is decreasing on
is decreasing on
 .
.
![]() also provides
information about the shape of the curve in terms of what is called
concavity. Concavity can also be defined in several ways. Geometrically,
it can be said that the graph of
also provides
information about the shape of the curve in terms of what is called
concavity. Concavity can also be defined in several ways. Geometrically,
it can be said that the graph of ![]() is concave up near a point
is concave up near a point
![]() if the tangent line at
if the tangent line at ![]() lies below the graph of
lies below the graph of ![]() on some
open interval containing
on some
open interval containing ![]() and is concave up if the tangent line
lies above the graph of
and is concave up if the tangent line
lies above the graph of ![]() on some open interval containing
on some open interval containing
![]() . Algebraically, concavity is most often defined by saying that
. Algebraically, concavity is most often defined by saying that ![]() is concave up on an interval
is concave up on an interval ![]() if
if ![]() is increasing on
is increasing on ![]() and is
concave down on
and is
concave down on ![]() if
if ![]() is decreasing on
is decreasing on ![]() . Using the theorem
above and remembering that
. Using the theorem
above and remembering that ![]() is the derivative of
is the derivative of ![]() gives the
following result.
gives the
following result.
![]() or is undefined, then substitute the critical value into the second derivative. If the second derivative is positive, then there is a relative minimum there and if the second derivative is negative, then there is a relative maximum there.
or is undefined, then substitute the critical value into the second derivative. If the second derivative is positive, then there is a relative minimum there and if the second derivative is negative, then there is a relative maximum there.
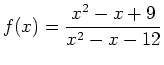 ,
,