Subsections

• Solving Equations
• The Limit Definition of the Derivative
• The Maple D and diff commands
• The Equation of a Tangent Line
• Finding Horizontal Tangents
• Exercises

Solving Equations and Differentiation

Solving Equations

The best method for solving equations is to use Maple's solving capabilities. First, a plot of the function or expression is useful then you can use the Maple solve command. The following illustrates how to find the roots of a function.

$$f(x) = 2x^3-5x^2-2x+5$$

> f := x-> 2*x^3-5*x^2-2*x+5;
> solve(f(x)=0,x);

If you forget to type in an equation and only type in an expression without setting it equal to something, Maple automatically sets the expression to zero. In the examples below, you can see some of the solving capabilities of Maple.

> plot({x^2+2*x-1,x^2+1},x=-2..2);
> solve(x^2+2*x-1=x^2+1,x);

Unfortuately, many equations cannot be solved analytically. For example, even the relatively simple equation sin(x) = x/2 has no analytical solution. In this case, the only possibility is to solve it numerically. In Maple, the command to use is fsolve. When the solve command is used the output looks like:

> solve(sin(x)=x/2,x);

This is not incorrect, as some of the zeros of a function may be imaginary and others may be real. However, it is much better to solve numerically as shown below:

> fsolve(sin(x) = x/2, x);

A plot of both equations on the same graph will show that this solution is not complete. There are two other intersection points that the fsolve command did not output. The fsolve command allows us to solve the equation in a range of $x$ values by replacing the second argument with what looks like a plot range. This method only works for the fsolve command and not for the solve command. To find the corresponding $y$ values of the intersection points, you only need to plug back into one of the functions.

> f:=x->sin(x);
> g:=x->x/2;
> plot({f(x),g(x)},x=-2*Pi..2*Pi);
> a:=fsolve(f(x)=g(x),x=-3..-1);
> b:=fsolve(f(x)=g(x),x=-1..1);
> c:=fsolve(f(x)=g(x),x=1..3);
> evalf(f(a));
> evalf(f(b));
> evalf(f(c));

Once you have solved an equation, you may want to use the output or the solution later. In order to label the output to a solution, you need to assign a label in the same line as the solve or fsolve command as seen above. It is different, however, if there is more than one output the the solve command. For example:

> f:=x->x^2+2*x-5;
> answer:=solve(f(x)=0,x);
> f(answer[1]);
> f(answer[2]);

Here an expression was defined first and then the solution was assigned to the label ``answer''. Note that there was more than one solution. In order to substitute the answer that was listed first back into the expression, the subs command was used and [1] was added onto the variable name to distinguish the first solution from the second.

The Limit Definition of the Derivative

The limit definition of the derivative of $f(x)$ often written as $f'(x)$ is defined as:

$$f'(x)=\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$$

The derivative of a function $f(x)$ at a point $x=a$, often written $f'(a)$, can be interpreted algebraically as the following limit

$$f'(a) = \lim_{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}$$

It can be interpreted geometrically as the slope of the tangent line to the graph of $f(x)$ at $x=a$ and functionally as the instantaneous rate of change of $f$ at $x=a$. Probably the second and third interpretations are the most important; they are certainly closer to what makes the derivative useful. In this lab, we will use Maple to explore each of these different aspects of the derivative. You can use the definition and the Maple limit command to compute derivatives directly, as shown below. You can also compute derivatives using Maple's diff or D command. The example below shows how to use the limit definition of derivative to find $f'(1))$ with Maple.

> f := x -> x^2+3*x+5;
> limit((f(1+h)-f(1))/h,h=0);

The following limit determines f'(x).

> limit((f(x+h)-f(x))/h,h=0);

The Maple D and diff commands

These commands can be summarized as follows.

• The D operator acts on a function to produce the derivative of that function.
• The diff command acts on an expression and differentiates that expression with respect to a variable specified by the user.

When you use the D operator to compute the derivative of a function, the result is also a function, as shown below.

> f:=x->x^2;
> D(f);

If you provide a label, then you get a function you can use later in the session,

> df := D(f);

However, this is usually not necessary. See the examples below.

If you want to evaluate the derivative at a specific value of $x$ or just get the expression for the derivative, you can use the following forms of the D operator.

> D(f)(2);
> D(f)(x);

This last form is the one to use for plotting, as shown below.

> plot(D(f)(x),x=-2..2);

The D operator cannot be used on expressions, for example trying to use it to differentiate the expresssion we defined above results in an error.

> p:=3*x+2;
> D(p);

If you recall that Maple uses f(x) to refer to the expresssion that is used to define $f$, then the following error shouldn't surprise you.

> D(f(x));

To differentiate expressions, you need to use the diff command. Here is an example.

> diff(p,x);

The diff command can also be applied to functions. However, the result of the diff command is an expression, not a function. This means that computing the value of the derivative at a specific value of $x$ requires you to use the subs command. The following example shows how to calculate $f'(2)$ using the diff command.

> df:=diff(f(x),x);
> subs(x=2,df);

The Equation of a Tangent Line

Suppose you want to find the equaton of the line tangent to the graph of $f(x)$ at the point $x=5$. This can be done in Maple using the point slope form of a line as shown below.

> tanline := D(f)(5)*(x-5)+f(5);
> plot{f(x),tanline},x=0..10);

Finding Horizontal Tangents

Combining Maple's capabilities for solving equations and finding derivatives, it should be very simple to find points on the graph of a functions where the tangent line is horizontal. For instance, the solve command finds the $x$ values where the horizontal tangents occur and plugging the $x$ values back into the function gives the corresponding $y$ values as seen in the example below. A plot of the derivative may be necessary to insure that you have found all zeros of the derivative. Remember, if the solve command fails, try fsolve.

> f := x-> 2*x^3-3*x^2-36*x+12;
> plot(D(f)(x),x=-10..10);
> solve(D(f)(x),x);
> f(-2);
> f(3);

Exercises

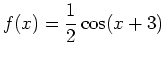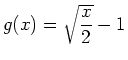1. For the functions $$f(x) = \frac{1}{2}\cos(x+3)$$ and $$g(x) = \sqrt{\frac{x}{2}}-1$$, plot both functions on the same graph using an $x$-domain that clearly shows all the intersection points and then find the $x$ and $y$ coordinates of the intersection points using Maple's solving capabilities.

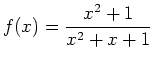2. Find the dervative of the function $$f(x)=\frac{x^2+1}{x^2+x+1}$$ using the limit definition of the derivative, the diff command and then the D command and then use all three methods to find the slope of 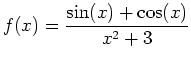$f$ at $x=0$.

3. Find the equation of the line tangent to the graph of the function $$f(x)=\frac{\sin(x)+\cos(x)}{x^2+3}$$ at $x=-2$. Include a plot of the function and the tangent line on the same graph over the interval $-4 \leq x \leq 0$.

4. For the function $$g(x)=x^3+11x^2-33x-22$$, find all $x$ values on the graph of $g(x)$ where the tangent line is horizontal.