


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The Absolute Extrema of a function on a closed interval is the highest and lowest point on the graph. That is for some value 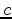 in the closed interval
in the closed interval ![$[a,b]$](img2.png) , if
, if 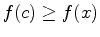 for all
for all ![$x \in [a,b]$](img4.png) , then
, then 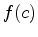 is the absolute maximum value and if
is the absolute maximum value and if
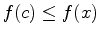 for all
for all ![$x \in [a,b]$](img4.png) , then
, then 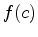 is the absolute minimum value.
is the absolute minimum value.
If 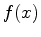 is a continuous function on the closed interval
is a continuous function on the closed interval ![$[a,b]$](img2.png) , then there exists numbers
, then there exists numbers 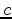 and
and 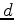 in the interval such that
in the interval such that 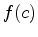 is the global minimum and
is the global minimum and 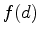 is the global maximum. If
is the global maximum. If 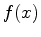 is not continuous, then it does not necessarily have an absolute maximum or an absolutr minimum value. One can check for continuity at questionable points by calculating the right and left handed limits. When
is not continuous, then it does not necessarily have an absolute maximum or an absolutr minimum value. One can check for continuity at questionable points by calculating the right and left handed limits. When 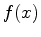 is continuous on
is continuous on ![$[a,b]$](img2.png) , we can find the absolute extrema either at a critical value
, we can find the absolute extrema either at a critical value 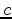 where
where 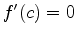 or
or 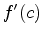 does not exist or at one of the endpoints
does not exist or at one of the endpoints 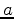 or
or 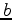 .
.
The Maple commands that are most useful are the ones for plotting
functions, taking derivatives, and solving equations. By plotting the
function and/or its derivatives, you can get a very good idea of approximately where the extrema occur. Then using the solve or fsolve commands you can find the values of 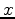 where
where 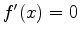 . Finally, you can use Maple to check the function value at each critical point and endpoint. The example below shows how Maple can be used to find the global extrema for
. Finally, you can use Maple to check the function value at each critical point and endpoint. The example below shows how Maple can be used to find the global extrema for
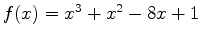 on the interval
on the interval ![$[-4,2]$](img17.png) .
.
> f := x-> x^3+x^2-8*x+1;
> plot(f(x),x=-4..2);
> solve(D(f)(x)=0,x);
> evalf(f(4/3));
> f(-2);
> f(-4);
> f(2);
The plot helps to see how many critical values you have. The solve command shows that there are critical values at 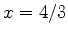 and
and 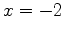 . Then evaluating the function at each critical value and each endpoint clearly shows that the absolute maximum is
. Then evaluating the function at each critical value and each endpoint clearly shows that the absolute maximum is 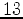 and occurs at the critical value
and occurs at the critical value 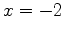 and the absolute minimum is
and the absolute minimum is 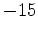 and occurs at the endpoint
and occurs at the endpoint 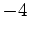 .
.
For each function below, find the absolute extrema on the given closed interval if they exist.
-
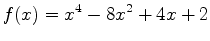 on
on
![$\displaystyle [-\frac{20}{25},\frac{64}{25}]$](img24.png) .
.
-
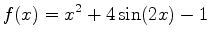 on
on ![$[-3,3]$](img26.png) .
.
-
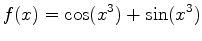 on
on
![$\displaystyle [\frac{\pi}{2},\frac{\pi}{2}]$](img28.png) .
.
-
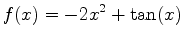 on
on ![$[0,1.5]$](img30.png) and
and ![$[0,5]$](img31.png) .
.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2010-11-16
![]() is a continuous function on the closed interval
is a continuous function on the closed interval ![]() , then there exists numbers
, then there exists numbers ![]() and
and ![]() in the interval such that
in the interval such that ![]() is the global minimum and
is the global minimum and ![]() is the global maximum. If
is the global maximum. If ![]() is not continuous, then it does not necessarily have an absolute maximum or an absolutr minimum value. One can check for continuity at questionable points by calculating the right and left handed limits. When
is not continuous, then it does not necessarily have an absolute maximum or an absolutr minimum value. One can check for continuity at questionable points by calculating the right and left handed limits. When ![]() is continuous on
is continuous on ![]() , we can find the absolute extrema either at a critical value
, we can find the absolute extrema either at a critical value ![]() where
where ![]() or
or ![]() does not exist or at one of the endpoints
does not exist or at one of the endpoints ![]() or
or ![]() .
.
![$\displaystyle [-\frac{20}{25},\frac{64}{25}]$](img24.png) .
.
![$\displaystyle [\frac{\pi}{2},\frac{\pi}{2}]$](img28.png) .
.