


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to give you experience using Maple to
compute derivatives to find tangent lines to an expression or function both explicitly and implicitly.
Suppose you want to find the equaton of the line tangent to the graph of 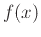 at the point
at the point 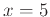 . Using the point slope form of a
line, this can be found and plotted in Maple as shown below.
. Using the point slope form of a
line, this can be found and plotted in Maple as shown below.
> f:=x->x^3;
> tanline := D(f)(3)*(x-5)+f(3);
> plot([f(x),tanline],x=0..6);
The implicitdiff command can be used to find derivatives of
implicitly defined functions. Suppose we wanted to use implicit
differentiation to find
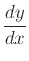 for the relation
for the relation
Then we first define our relation and give it a label for later use.
> f:=x^2+y^2=25;
A plot may be necessary to determine how many y values there are for a given x value. For instance, at 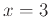 , we can show that
, we can show that 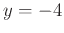 and
and 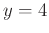 :
:
> with(plots):
> implicitplot(f,x=-6..6,y=-6..6);
> solve(subs(x=3,f),y)
The syntax of the implicitdiff command is shown by the
following example.
> der:=implicitdiff(f,y,x);
The result of the command is the implicit derivative,
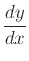 . The syntax of this command is very similar to that of
the diff command. The first argument is always the relation
that you want to differentiate implicitly. We were careful to use an
equation for this argument, but if you just give an expression for
this argument, Maple assumes you want to set this expression equal to
zero before differentiating. The second argument to the
implicitdiff command is where you tell Maple what the
dependent variable is. That is, by putting y here, we were
saying that we were thinking of this relation as defining
. The syntax of this command is very similar to that of
the diff command. The first argument is always the relation
that you want to differentiate implicitly. We were careful to use an
equation for this argument, but if you just give an expression for
this argument, Maple assumes you want to set this expression equal to
zero before differentiating. The second argument to the
implicitdiff command is where you tell Maple what the
dependent variable is. That is, by putting y here, we were
saying that we were thinking of this relation as defining 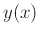 and
not
and
not 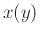 . The remaining arguments to implicitdiff are for
specifying the order of the derivative you want.
. The remaining arguments to implicitdiff are for
specifying the order of the derivative you want.
Second derivatives can also be computed with implicitdiff. The
following command computes
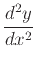 .
.
> der2:=implicitdiff(f,y,x,x);
To compute numerical values of derivatives obtained by implicit
differentiation, you have to use the subs command. For example, to
find the value of
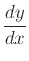 at the point
at the point 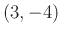 you could use the following command.
you could use the following command.
> m:=subs({x=3,y=-4},implicitdiff(f,y,x));
Suppose you wanted to find the equation of the tangent line to the graph of 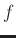 at the point
at the point 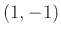 . You may want to label the output to
. You may want to label the output to
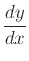 at the point
at the point 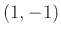 as
as 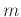 for slope and then you can use the point-slope form of a line to get the equation of the tangent line. The Maple commands below show how this can be done.
for slope and then you can use the point-slope form of a line to get the equation of the tangent line. The Maple commands below show how this can be done.
> m := subs({x=3,y=-4},implicitdiff(f,y,x));
> tanline := y-(-4)=m*(x-3);
> with(plots):
> implicitplot({f,tanline},x=-6..6,y=-6..6);
We can also use implicit differentiation to find higher order derivatives. For example, we may want to determine the concavity of a graph by evaluating the second derivative at a point as shown below:
> der2 := implicitdiff(f,y,x,x)
> subs({x=3,y=-4},der2)
- Given the relation
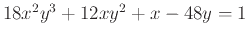 ,
,
- A)
- Define the equation as an expression
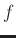 and plot the graph of the relation over the interval
and plot the graph of the relation over the interval
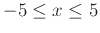 and
and
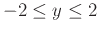 . How many
. How many 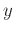 values are there at
values are there at 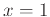 ? Find them using the solve command.
? Find them using the solve command.
- B)
- Find the slope of the graph at the point where
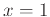 and
and 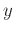 is negative. Label the slope as m.
is negative. Label the slope as m.
- C)
- Find the equation of the line tangent to the graph of the given relation at the point where
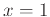 and
and 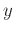 is negative. Be sure to label the tangent line as an implicit relation using the point-slope form of a line. Supply a plot of the relation and the tangent line over the intervals
is negative. Be sure to label the tangent line as an implicit relation using the point-slope form of a line. Supply a plot of the relation and the tangent line over the intervals
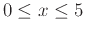 and
and
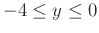 .
.
- Enter the following equation as expression
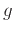 in Maple:
in Maple:
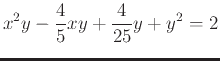 .
.
- A)
- Plot the relation
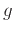 using the plotting intervals
using the plotting intervals
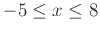 and
and
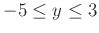 . Looking at the graph, how many points have the x value
. Looking at the graph, how many points have the x value
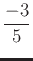 ? Using the solve command find the y value(s).
? Using the solve command find the y value(s).
- B)
- Find the slope of the tangent at each point and name them
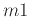 ,
, 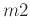 , ...
, ...
- C)
- Find the equation of the line(s) tangent to
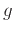 at each point and label them. Plot the relation and the tangent line(s) on the same graph using the same plotting intervals given above.
at each point and label them. Plot the relation and the tangent line(s) on the same graph using the same plotting intervals given above.
- D)
- Looking at your graph in part A, is the concavity positive or negative at each point whose x value is
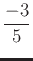 . Find
. Find
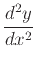 of each of the points to confirm.
of each of the points to confirm.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2019-11-13
![]() for the relation
for the relation
![]() . The syntax of this command is very similar to that of
the diff command. The first argument is always the relation
that you want to differentiate implicitly. We were careful to use an
equation for this argument, but if you just give an expression for
this argument, Maple assumes you want to set this expression equal to
zero before differentiating. The second argument to the
implicitdiff command is where you tell Maple what the
dependent variable is. That is, by putting y here, we were
saying that we were thinking of this relation as defining
. The syntax of this command is very similar to that of
the diff command. The first argument is always the relation
that you want to differentiate implicitly. We were careful to use an
equation for this argument, but if you just give an expression for
this argument, Maple assumes you want to set this expression equal to
zero before differentiating. The second argument to the
implicitdiff command is where you tell Maple what the
dependent variable is. That is, by putting y here, we were
saying that we were thinking of this relation as defining ![]() and
not
and
not ![]() . The remaining arguments to implicitdiff are for
specifying the order of the derivative you want.
. The remaining arguments to implicitdiff are for
specifying the order of the derivative you want.
![]() .
.
![]() at the point
at the point ![]() you could use the following command.
you could use the following command.
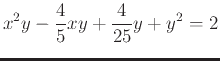 .
.