


Next: Exercises
Up: Newton's Method
Previous: Purpose
Many problems in mathematics, science, engineering, and business
eventually come down to finding the roots of a nonlinear equation.
It is a sad fact of life that many mathematical equations
cannot be solved analytically. You already know about the formula
for solving quadratic polynomial equations. You might not know,
however, that there are formulas for solving cubic and quartic
polynomial equations. Unfortunately, these formulas are so cumbersome
that they are hardly ever used. Even more unfortunately, it has been
proven that no formula can exist for finding roots of quintic or
higher polynomials. Furthermore, if your equations involve trig
functions, then it
is even easier to find equations that do not have analytical
solutions. For example, the following simple equation cannot be solved to
give a formula for x.
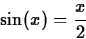
The need to solve nonlinear equations that cannot be solved
analytically has led to the development of numerical methods. One of
the most commonly used numerical methods is called Newton's method or
the Newton-Raphson method. The idea of Newton's method is relatively
simple. Suppose you have a nonlinear equation of the form
f(x) = 0
where f is a differentiable function. Then the idea of Newton's
method is to start with an initial guess x0 for the root and to use
the tangent line to f at x=x0 to approximate f. The equation
for the tangent line appears below.
y = f(x0)+f'(x0) (x-x0)
If the tangent line is a good approximation to f, then the x
intercept of the tangent line should be a good approximation to the
root. Call this value of x where the tangent line intersects the x
axis x1. We can solve the equation above to get the following
formula.
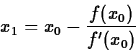
In practice, unless the starting point x0 is very close to
the root, the value x1 is not close enough to the root we are
seeking, so Newton's method is applied again using the tangent line at
x=x1. This process can be repeated, leading to a sequence of values
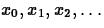 where the value of xn+1 is determined from the
equation
where the value of xn+1 is determined from the
equation
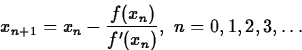
For example, consider the equation from above,
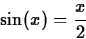
If you want to solve this equation using Newton's method, the first
thing to do is to write it in standard form as
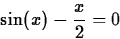
Then, plot the expression to get an idea of where the roots are. You
may have to adjust the plot range to locate all of the roots. The
following commands show that there are exactly three roots, one at
x=0, and two others at about 2 and -2.
> f := x -> sin(x)-x/2;
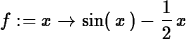
> plot(f(x),x=-6..6);
It isn't very hard to write a Maple command that will do one step of
Newton's method. The examples below show a very simple method for
doing so, using the function f defined above and a starting value of
x=2.2.
> newt := x -> x-f(x)/D(f)(x);
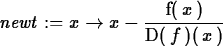
> newt(2.2);
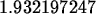
More steps can be obtained by using composition, as shown below. One
can even get a little fancier by using the Maple seq command
and the Maple composition operator,
as the last example below shows.
> newt(newt(2.2));
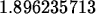
> (newt@@3)(2.2);
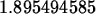
> seq((newt@@i)(2.2),i=1..4);
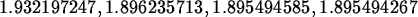
However, to simplify things for you, two commands, Newton and
NewtonPlot, have been programmed for you. The Newton
command takes three arguments: the function, the starting value, and
the number of iterations. See the example below for three iterations.
Note that these commands are part of the CalcP package, so
you must load the package first.
> with(CalcP):
> Newton(f,x=2.2,3);
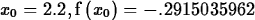
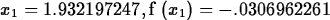
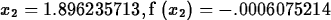
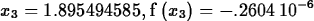
The NewtonPlot command gives a graphical representation of
Newton's method by plotting the function f and the sequence of
tangent lines on the same graph. It also shows vertical lines from the
x intercept for each tangent line to the graph of f. Here is an example.
> NewtonPlot(f,x=2.2);
One of the problems with Newton's method is knowing when to stop. With a
numerical method, you can never get a root exactly, but only a
numerical approximation to the root. There are basically two measures
of how good your approximation to the root is. One is the absolute value of
f(xn). If this number is less than a certain tolerance, then you
should have a good approximation to the root. The other measure is the
change in the value of xn. If the value of xn and xn+1 are
very close, then this can also be a criterion for stopping. You should
go back to the example above and experiment with changing the number
of iterations.
The worst thing about Newton's method is that it may fail to
converge. Here is an example that doesn't seem to be converging after
five iterations. Try increasing the number of iterations and see what happens.
> g := x -> x^5-12*x^4+3*x^3+7*x^2-2*x-1;
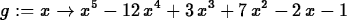
> plot(g(x),x=-2..2,y=-10..10);
> Newton(g,x=0,5);
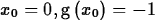
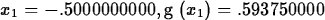
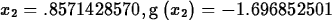
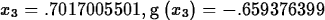
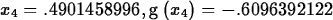
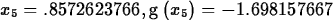
The key to getting Newton's method to converge is to select a good
starting value. The best way to do this is to plot the function and
determine approximately where the roots are. The use these values to
start Newton's method. For example, the following commands help locate
a root of g near x=-0.6 and then show that Newton's method
converges rapidly.
> plot(g(x),x=-2..2,y=-10..10);
> Newton(g,x=-0.6,5);
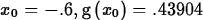
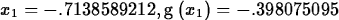
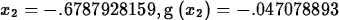
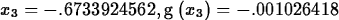
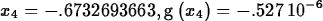
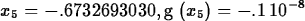



Next: Exercises
Up: Newton's Method
Previous: Purpose
William W. Farr
12/2/1997
![]()
![]()
![]()
![]()
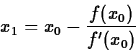
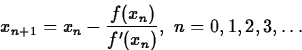
![]()
![]()