Exercises

1.

Use the Newton command with the function f from the examples and the starting value x=1.1.

(a)

Describe what happens when Newton's method is used with this initial condition. You might want to use NewtonPlot to help you understand what is going on. Start with just a few iterations, and then increase the number of iterations slowly. The maximum number of iterations you use should not exceed fifty.

(b)

What value of n is required to guarantee that 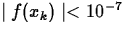$\mid f(x_k) \mid < 10^{-7}$ for all $k \geq n$?

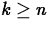2.

Use the Newton command to find an approximation to the root near x=-2 of the equation

$$\sin(x) = \frac{x}{2}$$

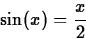
3.

Consider the function g from the examples.

(a)

Can you explain, using the graph of g and perhaps the NewtonPlot command, why Newton's method fails to converge for the initial guess x=0?

(b)

Find approximations to all of the roots of g. How do you know that you have found all of the roots?