Subsections

• Discussion
• Example 1. Approximation of $$\frac{45}{53}$$
• Example 2. Approximation of $x\sin(x)$ by x²
• Example 3. Approximation by a Polynomial
• Exercises

Approximation and Error Bounds

Discussion

The process of approximation is a central theme in calculus. (Chapter 10 of our text is devoted to this topic.) It gives a solution to the problem of computing difficult quantities:find an easily compute quantity which is sufficiently close to the desired quantity.

In the development of concepts as well as in numerous applications, a crucial step often involves approximating a given expression to within a stated accuracy. As you know, a function is a rule that assigns a definite value f(x) to each value x in the domain of f. To find the value of f(x) exactly, we must know x exactly. This point seems trivial until we realize that in many situations we have only approximations for x available! This reality is often the result of imperfections in measuring devices and other data-gathering mechanisms. More importantly, the necessity of approximation is an artifact of the number system and cannot be avoided. For example, the diagonal of the unit square has length $\sqrt{2}$. Although there exists an algorithm for computing the decimal expansion of the square root of two, it requires an infinite number of operations! Thus numerical expressions for $\sqrt{2}$ are, by necessity, approximations.

Every real number has an infinite decimal representation. Rational numbers are characterized as real numbers whose decimal expansions are eventually repeating. Irrational numbers are real numbers whose decimal expansions are non-repeating (such as $\sqrt{2}$). Decimal expressions for all irrational numbers and for most rational numbers are approximations. For example, 1.414 is an approximation to $\sqrt{2}$. Even when not working with irrational numbers, many of the numerical printouts of a calculator or computer approximations, since the machine only works with a limited number of digits of accuracy. (Look up the Digits command in Maple to see how to alter the number of digits, usually 10, that Maple prints for floating-point numbers.)

Approximations are also used in working with symbolic expressions. For example, for ``small'' values of x the expression $y = \sin(x)$ is often approximated by y = x when x is near zero. This means that when the value of x is near zero, the value of $\sin(x)$ is near the value of x. Another example is approximating a portion of a rational function by an asymptote. 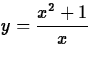For example, for ``large'' values of x the expression $y = \displaystyle\frac{x^2+1}{x}$ is approximated by y = x.

A basic question associated with any approximation is:How good is the approximation? That is, what is the error? Of course, no exact numerical description of the error can be given (otherwise there would be no need to use an approximation). Thus we introduce the term ``error bound,'' an upper bound on the size of the error. It is important to realize that although the absolute value of the error may be considerably smaller than the error bound, it can never be larger. In general, the smaller the error bound the better the approximation. Accuracy, abbreviated ACC (or by the Greek letter $\epsilon$), is often used as a synonym for error bound.

Sometimes the degree of accuracy needed in an approximation is specified by saying that it must be accurate to a given number of decimal places. One says that a, an approximation to a quantity s, is accurate to k decimal places if

This means that the true value of s lies between $a - \frac{1}{2} 10^{-k}$ and $a + \frac{1}{2} 10^{-k}$. Usually (but because of roundoff error, not always) this means that the first k decimal places in a are accurate.

Example 1. Approximation of $$\frac{45}{53}$$

We will approximate $$\frac{45}{53}$$ with ACC = 10^-3.

Using a calculator or Maple, we find the decimal expansion for $$\frac{45}{53}$$.

The desired approximation is 0.849. Note that the error is less and 10^-3. That is,

Actually the error in the above approximation is less than 10^-4.

Example 2. Approximation of $x\sin(x)$ by x²

We will determine an interval over which x² approximates $x\sin(x)$ with an accuracy of 0.1 or less. That is, determine an interval over which $\mid x \sin(x) - x^2 \mid < 0.1.$ We first transform this problem into one of finding the zeros of a function and then use a graphical approach to approximate the zeros.

Since $\mid x \sin(x) - x^2\mid < 0.1$ is equivalent to $\mid x \sin(x) - x^2 \mid - 0.1 < 0,$ we define a function f by $f(x) = \mid x\sin(x) - x^2 \mid - 0.1$ and determine the interval over which f(x) is negative. This is done by plotting f and determining (approximating) the zeros. If this is done, it is seen that the zeros can be approximated by -0.88 and 0.88. Thus x² approximates $x\sin(x)$ over the interval [-0.88,0.88] with an accuracy of 0.1.

Example 3. Approximation by a Polynomial

In this example we will find a quadratic polynomial that approximates the cosine function over the interval $\left[-\displaystyle\frac{\pi}{2}, \frac{\pi}{2}\right],$ and will estimate the error in the approximation. We define a general quadratic polynomial function:

  > p:=x->a*x^2+b*x+c;

We need three equations to solve for a,b, and c. To obtain them we will set p equal to cos at three points, $x = -\displaystyle\frac{\pi}{2}, x = 0,$ and $x = \displaystyle\frac{\pi}{2}$ and then apply the solve command to solve this system of equations for a, b, and c.

  > solve({p(-Pi/2)=cos(-Pi/2),p(0)=cos(0),p(Pi/2)=cos(Pi/2)},{a,b,c});

(As with other commands solve will work on a set of expressions, returning a set as an answer. Notice that in Maple's notation, if the order of items does not matter, then set notation is used:$\{a,b\;\; c\}$. If order does matter, then list notation is used: [a,b,c].) Now we substitute these values into p giving the desired polynomial which we call q:

  > q:=subs(``,p(x));

(Notice that p is a function; p(x) is p evaluated at x, an expression. The result of substituting values for $a,\;b,$ and c in the expression p(x) is the expression q.) We can estimate the error by graphing the difference between cos and q over the interval $\left[-\displaystyle\frac{\pi}{2}, \frac{\pi}{2}\right]$.If this is done, it can be seen from the plot that the error is at most 0.06.

Exercises

1.

Prove or disprove that 10^-4 is an error bound when $$\frac{41}{63}$$ is used to approximate 0.6502187492....

2.

Plot the graphs of $y = \sin(x)$ and y = x on the same set of axes. What information can you get from this plot? Next, use the approach of Example 2 to determine an interval centered at x = 0 over which y = x approximates $y = \sin(x)$ with 1 decimal place accuracy.

3.

Estimate the error when the sine function is approximated over the interval $\left[-\displaystyle\frac{\pi}{2}, \frac{\pi}{2}\right]$ by

(a)

a quadratic polynomial

(b)

a cubic polynomial

Which of these two polynomials better approximates the sine function over the given interval? Carefully explain the reasons for your answer.

4.

Determine whether y = x² or y = x³ is a better approximation to $y = \tan(x)$ over the interval [0,1]. Carefully explain the reasons for your choice.