Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for
![]()
![]()
![]()
Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Maple knows how to take many derivatives. Its main commands for doing this are D and diff. D is designed to differentiate functions, whereas diff is for differentiating expressions. However, if proper notation is used, diff can also be used with functions. To review the difference between a function and an expression, check the two examples below. The f statement defines a function, the g statement defines an expression.
> f:=x->x^2+7*x+5;
> g:=x^3-5*x+8;Here are some examples that show how D and diff work. Check the difference between these two commands.
> D(sin);
> D(sin)(x);Also, check these two.
> D(f);
> D(f)(x);Carefully consider these.
> diff(g,x);
> diff(f(x),x);See what happens with these.
> diff(g(x),x);
> diff(f,x);After the last four examples, you should be convinced that proper notation is very important in doing derivatives in Maple.
Maple can also do higher derivatives. Check these commands.
> diff(g,x2);
> diff(f(x),x$2);The $ sign is used to indicate repeated differentiation, the number following it tells how many times the function or expression is to be differentiated. D will also do repeated differentiation.
> (D@@2)(f)(x);
> diff({sin(x)^2,sin(x^2)},x);
However, note that while Maple does what is asked, it rearranges the
order of the output. So, be careful.
More information on diff and D can be obtained through Maple help screens.
> (f@f)(x);
> simplify(");
> h:=x->x^3+x^2-3*x+4;
> p:=x->8*x+6;
> (f@h@p)(x);
> simplify(");
> (p@h@f)(x);
> simplify(");
Are The implicitdiff command can be used to find derivatives of implicitly defined functions. The syntax is as follows
> implicitdiff(f,y,x);where f is an expression or equation, y is the dependent variable and x is the independent variable. Thus the command as just stated would compute
> f:=x^2*y^2+y^3;
> implicitdiff(f,y,x);
> g:=x^2+y^3=1;
> implicitdiff(g,y,x);Second derivatives can also be taken with implicitdiff. The following command computes
> implicitdiff(g,y,x,x);Maple also has a command for plotting implicitly defined functions. It is in the package plots which must be called before using the command.
> with(plots);
> implicitplot(x^2-y^2=1,x=-3..3,y=-3..3);
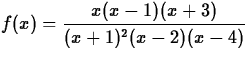 . What appears to
be true about the slope of the tangent line at each local minimum or
maximum point?
. What appears to
be true about the slope of the tangent line at each local minimum or
maximum point?
Christine Marie Bonini