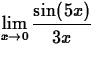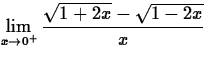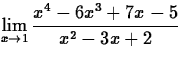Subsections

• MAPLE THROWS YOU FOR A LOOP
• Exercises

Some Ideas of Differential Calculus

MAPLE THROWS YOU FOR A LOOP

In Maple, loops can be used to generate much output with the input of only a few commands. Try the following code and see how it generates a list of the squares of the first six positive integers. Note that only the last line has a semicolon at the end. Because of this, after entering the first line you may get an error message

Warning, incomplete statement or missing semicolon.

Just ignore the warning and continue with the input.

  > for n from 1 to 6 do

  > print(n^2)

  > od;

if you want to print n and n² on the same line, change the second line to read

  > lprint(n,n^2)

If you want to put labels on the output, try

  > for k from 1 to 6 do

  > lprint(`k = `,k,`  k^4= `,k^4)

  > od;

(There are additional ways to get ``pretty'' output.) As you see, any expression enclosed in the ` marks will be printed exactly as written.

Loops can also be nested. The following code can be used to check on some of the functional values of 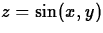$z = \sin(x,y)$.

  > for x from 1 to 3 by 0.5 do

  > for y from 1 to 3 by 0.5 do

  > lprint(x,y,sin(x*y))

  > od

  > od;

Exercises

1.

Type all commands given in the introductory section and display the output that results.

2.

In this exercise we consider plots of the function f(x) = x⁴ - 104x over intervals centered on x = 3.

(a)

Use a Maple loop to generate plots of the kind just mentioned. First set h = 1.0. Then set up a loop that will give six plots. The second line in the commands for the loop will by a plot statement for f(x) over the interval [3 - h, 3 + h]. (Note that Maple will insist that you put a semicolon at the end of this line.) On the next line set a new value of h that is 0.25 times the previous value - this will make the next plot be given over a smaller interval. Finally, finish the loop statement with an od.

(b)

Look at the y-scale on the last three plots. Do these numbers make sense? Explain what is going on with Maple.

(c)

Describe what has happened in the successive plots. What shape does the last graph appear to have? What slope is associated with the last graph? (Be careful since the x-axis and y-axis readings are on different scales. Show your computations.)

(d)

What do the results you described in (c) have to do with the basic ideas of differential calculus? Explain fully.

3.

Look up the syntax for the Maple limit command. Use that command to evaluate the following limits.

(a)

$$\lim_{x\rightarrow 0}\displaystyle\frac{\sin(5x)}{3x}$$

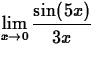
(b)

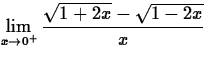
$$\lim_{x\rightarrow 0^+} \displaystyle\frac{\sqrt{1+2x}-\sqrt{1-2x}}{x}$$

(c)

$$\lim_{x\rightarrow 1}\displaystyle\frac{x^4-6x^3+7x-5}{x^2-3x+2}$$

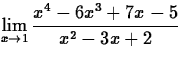
4.

Consider 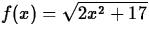$f(x) = \sqrt{2x^2+17}$ with c = 4.

(a)

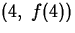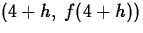Set up a statement for the slope of the secant line between the points $(4,\; f(4))$ and $(4 + h,\; f(4 + h))$. Use Maple to find the limit of this expression as h goes to 0.

(b)

Use a loop to evaluate your statement for the slope of the secant line at six small values of h.

(c)

Explain the geometric significance of what you have done in (a) and (b). Relate the work of this exercise to the answer you gave for 2(d).

5.

Suppose the number of bacteria in a certain organism grows over time and the number, N(t), of bacteria (measured in thousands) at time t (in days) is given by

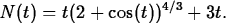
At any given time t the number of bacteria is actually an integer, and here we are approximating the number by the value N(t).

(a)

Plot N(t) for the interval [0,10]. From inspection of the graph, choose the integer value of t, t₀, at which it appears that the number of bacteria is increasing most rapidly. Calculate the average growth rate from t = t₀ to t = t₀ + 0.5.

(b)

Write an expression giving the average growth rate over the time interval [t₀, t₀ + h].

(c)

Take the limit as h goes to 0 of your expression from (b). Interpret this limit. Explain its significance.