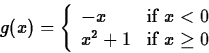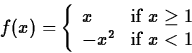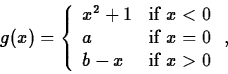

Next: About this document ...
Up: No Title
Previous: No Title
Subsections
The purpose of this lab is to use Maple to become more familiar with
limits of functions, including one-sided limits.
Limits of many functions and expressions can be computed in Maple with
the limit command. Some examples are given below.
> limit(x^2+2*x,x=2);
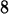
> limit(sin(x)/x,x=0);
> f := x -> (x+3)/(x^2+7*x+12) ;
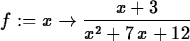
> limit(f(x),x=-3);
> limit(f(x),x=-4);
If the limit exists, Maple can usually
find it. In cases where the limit doesn't exist, Maple gives the
answer infinity for an unbounded limit or gives a range like
-1..1 if the limit doesn't exist, but the expression or
function is bounded. See the examples below.
> limit(1/x,x=0);
> limit(sin(1/x),x=0);
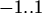
You can also use Maple to compute limits as x goes to 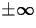 as shown below.
as shown below.
> f(x);
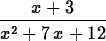
> limit(f(x),x=infinity);
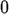
> limit(f(x),x= -infinity);
The formal definition for a limit is given below.
Definition 437
We say that the number L is the limit of
f(x) as x approaches a provided that, given any number
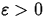 , there exists a number
, there exists a number 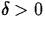 such that
such that
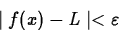
for all x such that
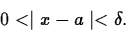
This definition may seem
complicated, but its graphical interpretation is not so bad. It says
that if you plot f(x) - L with the y range set to
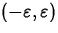 you can always choose a value of
you can always choose a value of 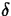 small enough so that when you shrink the x plot range to
small enough so that when you shrink the x plot range to
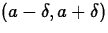 and plot the function, its graph will not
intersect the top or the bottom edges of your plot. For example,
suppose f(x)=x2, a=2 and
and plot the function, its graph will not
intersect the top or the bottom edges of your plot. For example,
suppose f(x)=x2, a=2 and 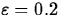 . Then any value of
. Then any value of
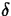 smaller than about 0.049 will work. To see what is going
on, look at the plots generated by the following commands.
smaller than about 0.049 will work. To see what is going
on, look at the plots generated by the following commands.
> f := x -> x^2;
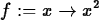
> limit(f(x),x=2);
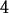
> L := 4; epsilon := 0.2; delta := 0.1;
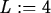
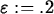
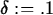
> plot({-epsilon, epsilon, f(x) - L},x=2-delta..2+delta);
> delta := 0.048;
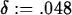
> plot({-epsilon, epsilon, f(x) - L},x=2-delta..2+delta);
In the first of the two plot commands, the value of  is
0.1. This is too large, since the graph intersects the lines
y=-0.2 and y=0.2. The value of 0.048 for
is
0.1. This is too large, since the graph intersects the lines
y=-0.2 and y=0.2. The value of 0.048 for  in the second
plot command, however, is small enough, since the graph of
f(x) goes off the sides of the plot. Make sure that you understand
this example. If you don't understand, ask for help. Note that by
using labels for the values of L,
in the second
plot command, however, is small enough, since the graph of
f(x) goes off the sides of the plot. Make sure that you understand
this example. If you don't understand, ask for help. Note that by
using labels for the values of L, 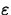 , and
, and 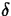 , we
were able to use the same plot command. By copying and pasting, you can
save yourself some typing. Using labels also helps prevent errors.
It should be no secret by now that for most
functions f(x) defined by a single formula,
, we
were able to use the same plot command. By copying and pasting, you can
save yourself some typing. Using labels also helps prevent errors.
It should be no secret by now that for most
functions f(x) defined by a single formula, 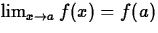 when f(a) exists. For more complicated functions, this
may not be true. For dealing with some of these exceptional cases, we
need to define right-hand and left-hand limits. Loosely speaking, the
right-hand limit of f(x) at a is L if f(x) approaches L as
x approaches a from the right. That is, the values of x satisfy
x > a. The left-hand limit is defined in an analogous manner, with
the values of x approaching a from the left. Maple can
compute these special limits with commands like those shown below. The
Maple floor function is actually the greatest integer function.
when f(a) exists. For more complicated functions, this
may not be true. For dealing with some of these exceptional cases, we
need to define right-hand and left-hand limits. Loosely speaking, the
right-hand limit of f(x) at a is L if f(x) approaches L as
x approaches a from the right. That is, the values of x satisfy
x > a. The left-hand limit is defined in an analogous manner, with
the values of x approaching a from the left. Maple can
compute these special limits with commands like those shown below. The
Maple floor function is actually the greatest integer function.
> plot(floor(x),x=0..4);
> limit(floor(x),x=1,right);
> limit(floor(x),x=1,left);
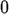
The floor function is one of Maple's defined functions, so you
might expect things to work properly. If you want to define your own
piecewise-defined function, then the Maple piecewise command
is the best way to do it. Suppose you wanted to define the following
function.
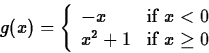
Then the Maple command would be the following.
> g := x -> piecewise(x < 0, -x, x^2+1);
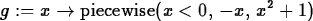
The way the piecewise command works is that you give it a
sequence of pairs of conditions and formulas that define your
function. When you want to evaluate your function at a particular
value of x, Maple checks the conditions from left to right until it
finds the one that your value of x satisifies. It then plugs the
value of x into the next formula. However, notice that the command
above only has one condition and two formulas. This is because any
value of x is either less than zero or it is greater than or equal
to zero, so if a particular value of x fails the first condition,
i.e. is not less than zero, it must be greater than or equal to zero
and the second formula is the one to use. For more information, see
the help page for piecewise.
The limit command works fine for functions that are defined
via the piecewise command, as shown in the example below.
> limit(g(x), x=0);
> limit(g(x),x=0, left);
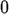
> limit(g(x),x=0, right);
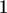
> plot(g(x), x=-0.1..0.1);
- 1.
- For the functions and values of a given below, go through the
following steps.
- i.
- Find whether the
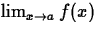 exists or
not. If it does, determine the limit.
exists or
not. If it does, determine the limit.
- ii.
- For the limits that exist, find a value of
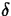 that
works for
that
works for 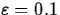 . The
. The 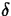 value should be close to its maximum value.
value should be close to its maximum value.
- (a)
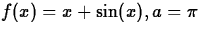 .
.- (b)
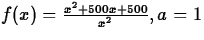
- (c)
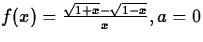
- (d)
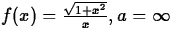
- (e)
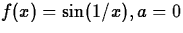
- 2.
- Find the right- and left-hand limits of the following function at
x=1. Also, plot the function and
relate your limits to the graph.
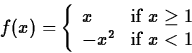
Does 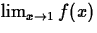 exist? Explain your reasoning.
exist? Explain your reasoning.
- 3.
- Suppose that the function g(x) is defined by
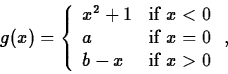
where a and b are parameters. Can you find values for a and b
that will make g(x) continuous at x=0? Justify your answer.


Next: About this document ...
Up: No Title
Previous: No Title
Jane E Bouchard
11/9/1999
![]()
![]()
![]()
![]() , there exists a number
, there exists a number ![]() such that
such that
![]()
![]()
![]() you can always choose a value of
you can always choose a value of ![]() small enough so that when you shrink the x plot range to
small enough so that when you shrink the x plot range to
![]() and plot the function, its graph will not
intersect the top or the bottom edges of your plot. For example,
suppose f(x)=x2, a=2 and
and plot the function, its graph will not
intersect the top or the bottom edges of your plot. For example,
suppose f(x)=x2, a=2 and ![]() . Then any value of
. Then any value of
![]() smaller than about 0.049 will work. To see what is going
on, look at the plots generated by the following commands.
smaller than about 0.049 will work. To see what is going
on, look at the plots generated by the following commands.
![]()
![]()