

Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Subsections
The purpose of this lab is to teach you how to use Maple commands for
computing derivatives.
Maple has several commands for computing derivatives. The most common
ones are the diff command for differentiating expressions and
the D operator for differentiating expressions. These are the
commands we will consider here.
Before introducing the commands for differentiation, we need to review
the concepts of expression and function in Maple. An
expression is a collection of mathematical symbols, for
example 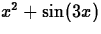 and x2-y2 are both expressions. A function,
on the other hand, is a rule for associating an output value with an
input value.
and x2-y2 are both expressions. A function,
on the other hand, is a rule for associating an output value with an
input value.
The connection is that expressions are often used to define a
function. That is, we could let 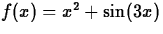 , which defines a
function f. The rule for this function is to substitute a value for
x into the expression
, which defines a
function f. The rule for this function is to substitute a value for
x into the expression 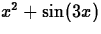 to obtain the output value. Not
all expressions can be used to define functions, however, and not all
functions are defined by expressions so these really are distinct
mathematical objects.
to obtain the output value. Not
all expressions can be used to define functions, however, and not all
functions are defined by expressions so these really are distinct
mathematical objects.
Maple mimics this mathematical distinction between expression and
function. You can define expressions in Maple and even label them for
later use with commands like the one below.
> p := x^2+sin(3*x);
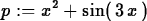
This is an expression not a function, which means there is no rule
associated with it. Thus evaluating the expression at a specific value
of x requires the subs command, as in the following
example.
> subs(x=2,p);
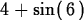
The syntax for defining a function in Maple uses an arrow to make the
idea of a function as a process explicit. For example, we can define a
function f in Maple using the expression 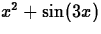 with the
following command.
with the
following command.
> f := x -> x^2+sin(3*x);
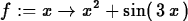
Evaluating our function at a specific value of x is now easy.
> f(2);
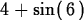
One final thing to note is that Maple will use f to denote
the function we have defined, but will use f(x) to denote the
expression used to define the function.
Students often want to define a function with a command like the following.
> F(x) := x^2+3;
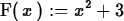
Since Maple doesn't complain, students often think that what they've
done is correct. The output from the following commands, however,
shows that the object we've defined doesn't behave like a function.
> F(x);
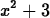
> F(1);
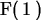
> F(t);
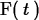
> F(2*x);
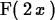
What is happening here is that we've defined something called a
table in Maple. For the input x it gives the output
x2+3, but it doesn't behave like a function and doesn't give the
value we wanted for any other input.
These commands can be summarized as follows.
- The D
operator acts on a function to produce the derivative of that
function.
- The diff command acts on an expression and
differentiates that expression with respect to a variable specified by
the user.
When you use the D operator to compute the derivative of a
function, the result is also a function, as shown below.
> D(f);
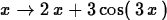
If you provide a label, then you get a function you can use later in
the session,
> df := D(f);
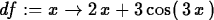
However, this is usually not necessary. See the examples below.
If you want to evaluate the derivative at a specific value of x or
just get the expression for the derivative, you can use the following
forms of the D operator.
> D(f)(2);
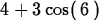
> D(f)(x);
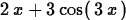
This last form is the one to use for plotting, as shown below.
> plot(D(f)(x),x=-2..2);
The D operator cannot be used on expressions, for example
trying to use it to differentiate the expresssion we defined above
results in an error.
> D(p);
Error, (in D) univariate operand expected
If you recall that Maple uses f(x) to refer to the
expresssion that is used to define f, then the following error
shouldn't surprise you.
> D(f(x));
Error, (in D) univariate operand expected
To differentiate expressions, you need to use the diff
command. Here is an example.
> diff(p,x);
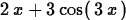
The diff command can also be applied to functions as shown
below.
> diff(f(x),x);
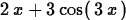
Note, however, that the result of the diff command is an
expression, not a function. This means that computing the value of the
derivative at a specific value of x requires you to use the
subs command.
In this subsection, we compute the tangent line at 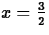 to
our function f using first the D operator and then the
diff command. This gives one example where the D
operator is probably easier to use than the diff command.
to
our function f using first the D operator and then the
diff command. This gives one example where the D
operator is probably easier to use than the diff command.
To find the tangent line at 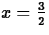 to our function f, we
need two pieces of information. One is the slope of the tangent line,
which is given by
to our function f, we
need two pieces of information. One is the slope of the tangent line,
which is given by 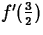 , and the other is a point on the
line, which is
, and the other is a point on the
line, which is 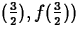 . Then, using the
point-slope formula, the equation for the tangent line is
. Then, using the
point-slope formula, the equation for the tangent line is
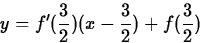
Implementing this using the D operator is relatively simple,
as shown below.
> tf := x -> D(f)(3/2)*(x-3/2)+f(3/2);
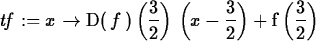
> plot({f(x),tf(x)},x=0..3);
Using the diff command to compute the tangent line is a
little harder, because the subs command must be used.
> tf2 := x -> subs(x=3/2,diff(f(x),x))*(x-3/2)+f(3/2);
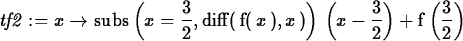
> plot({f(x),tf2(x)},x=0..2);
- 1.
- Give an example of a situations where the D operator
would be easier to use than the diff command. Then give an
example where the diff command would be better. In each case,
make sure you justify your choice.
- 2.
- Use either the D or diff commands to find the
derivative of the following function. Plot the graph of the
derivative over the given range and evaluate the derivative at the
indicated point.
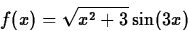
Graph for 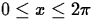 . Evaluate at
. Evaluate at 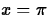 .
. - 3.
- Consider the function
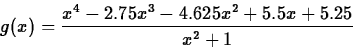
Find all of the points where the derivative of g is equal to 1.
- 4.
- The tangent line to a function at a particular value of x
intersects the graph of the function at least once, at the point of
tangency. However, the tangent line may intersect the graph at other
points. In this problem, we investigate whether the tangent line at
one point can also be tangent to the graph at another point. For
example, consider the function
g(x) = (x2-1)2
Show that the tangent line at x=-1 is also
tangent to the graph at x=1.
Next, suppose we change the function slightly.
h(x) = (x2-1)2 +x/2
Is it still possible to find two different values of x such that the
tangent lines coincide? The answer is yes. Find them.


Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Jane E Bouchard
2/1/2000
![]()
![]()
![]()
![]() , which defines a
function f. The rule for this function is to substitute a value for
x into the expression
, which defines a
function f. The rule for this function is to substitute a value for
x into the expression ![]() to obtain the output value. Not
all expressions can be used to define functions, however, and not all
functions are defined by expressions so these really are distinct
mathematical objects.
to obtain the output value. Not
all expressions can be used to define functions, however, and not all
functions are defined by expressions so these really are distinct
mathematical objects.
![]() to our function f, we
need two pieces of information. One is the slope of the tangent line,
which is given by
to our function f, we
need two pieces of information. One is the slope of the tangent line,
which is given by ![]() , and the other is a point on the
line, which is
, and the other is a point on the
line, which is ![]() . Then, using the
point-slope formula, the equation for the tangent line is
. Then, using the
point-slope formula, the equation for the tangent line is
![]()
![]()
![]()