


Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Subsections
Suppose that f(x) is a differentiable function. Then we
know that the value of f'(x) gives the slope of the tangent
line at x. Geometrically, the slope of the tangent line at a
particular point x=a tells us whether the value of the function is
increasing, decreasing, or staying the same as we look at
values of x near a. In applications, one is often trying to find
the minimum or maximum values of a function so it turns out to be
important to be able to determine when a function is increasing and
when it is decreasing. Mathematically, we say that a function is
increasing on an interval I if x1 < x2 means f(x(1) < f(x2)
for every pair of numbers x1,x2 in I. Conversely, we we say that
a function is
decreasing on an interval I if x1 < x2 means f(x(1) > f(x2)
for every pair of numbers x1,x2 in I. These are the definitions
of increasing and decreasing functions, but they are not very easy to
apply. Most often, we use the first derivative as described in the
following theorem.
Theorem 346
Suppose f is continuous on an interval I and differentiable at
every interior point of I.
- 1.
- If f'(x) > 0 on the interior of I, then f is increasing on
I.
- 2.
- If f'(x) < 0 on the interior of I, then f is decreasing on
I.
This theorem says that we can determine when a function is
increasing or decreasing by solving the inequalities f'(x) > 0 and
f'(x) , 0. In practice, we usually work with functions having
continuous derivatives, which means that f' can change sign only at
a point where f'(x)=0. For example, consider f(x) = x2. The
derivative is f'(x) = 2x, which is zero only at x=0. This critical
point divides the real line up into two intervals, x<0 and
x>0. Since f' can never be zero if 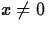 , the sign of f'(x)
is constant on each interval. That is for x<0 we have f'(x) = 2x
<0 so f is decreasing for x<0. Similarly, f is increasing for
x>0. This suggests the following procedure for determining where a
function is increasing or decreasing.
, the sign of f'(x)
is constant on each interval. That is for x<0 we have f'(x) = 2x
<0 so f is decreasing for x<0. Similarly, f is increasing for
x>0. This suggests the following procedure for determining where a
function is increasing or decreasing.
- 1.
- Find the critical points of f. Note that according to the
definition in the text, critical points of f are points where either
f' is zero, the derivative doesn't exist, or endpoints of I if f
is defined on a finite interval I.
- 2.
- The critical points divide the domain of f into subintervals
on which the sign of f' is constant. Check the sign of f' at one
interior point on each subinterval. If it is positive, f is
increasing on that subinterval. If it is negative, f is decreasing
on that subinterval.
The second derivative, f''(x) also provides
information about the shape of the curve in terms of what is called
concavity. Concavity can also be defined in several ways. Geometrically,
it can be said that the graph of f is concave up near a point
x=a if the tangent line at x=a lies below the graph of f on some
open interval containing a and is concave up if the tangent line
lies above the graph of f on some open interval containing
c. Algebraically, concavity is most often defined by saying that f
is concave up on an interval I if f' is increasing on I and is
concave down on I if f' is decreasing on I. Using the theorem
above and remembering that f'' is the derivative of f' gives the
following result.
Theorem 403
Suppose f be twice differentiable on the open interval I.
- 1.
- If f''(x) > 0 on I, then f is concave up on
I.
- 2.
- If f''(x) < 0 on I, then f is concave down on
I.
This means that we can find where f is concave up and concave down
using the same procedure on f'' that we used on
f'. That is, we first find all of values of x for which f''(x)=0, or
f''(x) doesn't exist. Including the endpoints, if our domain is a
finite interval, these values of x are the endpoints of distinct
subintervals on which the sign of f'' is constant. Checking the sign
of f'' at one point in the interior of each subinterval determines
the concavity of f on that subinterval.
The Maple commands that are most useful are the ones for plotting
functions, taking derivatives, and solving equations. By plotting the
function and/or its derivatives, you can get a very good idea of where
it is increasing/decreasing and where it is concave up/concave
down. Then using the solve or fsolve commands
you can find the values of x where f'(x)=0 or f''(x)=0. Finally,
you can use Maple to check the signs of f' or f'' in the interior
of the subintervals. Examples are in the Getting Started
worksheet. This worksheet will make this lab a lot easier to complete,
so you should go through it carefully before beginning the exercises.
- 1.
- Suppose f id continuously differentiable and c is a number
such that f'(c)=0. Is it necessarily true that f is increasing in
some interval on one side of c and decreasing in some interval on
the other side of c?
- 2.
- For the following functions, find the intervals on which they
are increasing and the intervals on which they are decreasing.
- (a)
- f(x) = x3-4x+1.
- (b)
- f(x) = x4-23x3+59x2+23x-60.
- (c)
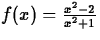 .
.- (d)
- f(x) = x+sin(x).
- (e)
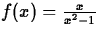
- 3.
- For the following functions, find the intervals on which they
are concave
upward and the intervals on which they are concave downward. Make sure
that you
explain how you got your results.
- (a)
- f(x) = x3-4x+1.
- (b)
- f(x) = x4-23x3+59x2+23x-60.
- (c)
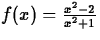 .
.- (d)
- f(x) = x+sin(x).
- (e)
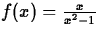



Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Jane E Bouchard
2/15/2000
![]()
![]()
![]()
![]() , the sign of f'(x)
is constant on each interval. That is for x<0 we have f'(x) = 2x
<0 so f is decreasing for x<0. Similarly, f is increasing for
x>0. This suggests the following procedure for determining where a
function is increasing or decreasing.
, the sign of f'(x)
is constant on each interval. That is for x<0 we have f'(x) = 2x
<0 so f is decreasing for x<0. Similarly, f is increasing for
x>0. This suggests the following procedure for determining where a
function is increasing or decreasing.