Subsections

• Purpose
• Background
• The limit definition of the derivative
  • The Maple D and diff commands
  
  
• Exercises

Derivatives

Purpose

The purpose of this lab is to teach you how to use Maple commands for computing derivatives.

Background

You can compute derivatives in Maple using the limit definition of the derivative and Maple's limit command. The more common methods of computing derivative in Maple are the diff command for differentiating expressions and the D operator for differentiating functions. We will compute derivatives using all three methods.

The limit definition of the derivative

Using the definition of derivative

$$\lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$$

, you can do this in Maple by first defining the difference quotient and the computing the limit. The following example shows how to compute the derivative of 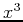$x^3$ and the evaluate the derivative at $x=-2$.

> f:=x-> x^3;
> quot := (f(x+h)-f(x))/h;
> der:=limit(quot,h=0);
> subs(x=-2,der);

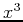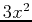or if you don't need to see that the derivative of $x^3$ is $3x^2$ and you just want to evaluate the derivative at $x=-2$, then this could be done all in one Maple command as in the following example:

> f:=x->x^3;
> limit((f(-2+h)-f(-2))/h,h=0));

The Maple D and diff commands

These commands can be summarized as follows.

• The D operator acts on a function to produce the derivative of that function.
• The diff command acts on an expression and differentiates that expression with respect to a variable specified by the user.

When you use the D operator to compute the derivative of a function, the result is also a function, as shown below.

> D(f);

If you provide a label, then you get a function you can use later in the session,

> df := D(f);

However, this is usually not necessary. See the examples below.

If you want to evaluate the derivative at a specific value of 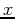$x$ or just get the expression for the derivative, you can use the following forms of the D operator.

> D(f)(2);
> D(f)(x);

This last form is the one to use for plotting, as shown below.

> plot(D(f)(x),x=-2..2);

Suppose you want to find the equaton of the line tangent to the graph of 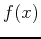$f(x)$ at the point 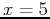$x=5$. This can be done in Maple using the point slope form of a line as shown below.

> tanline := D(f)(5)*(x-5)+f(5);

The D operator cannot be used on expressions, for example trying to use it to differentiate the expresssion we defined above results in an error.

> D(p);

If you recall that Maple uses f(x) to refer to the expresssion that is used to define 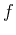$f$, then the following error shouldn't surprise you.

> D(f(x));

To differentiate expressions, you need to use the diff command. Here is an example.

> diff(p,x);

The diff command can also be applied to functions as shown below.

> diff(f(x),x);

Note, however, that the result of the diff command is an expression, not a function. This means that computing the value of the derivative at a specific value of 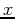$x$ requires you to use the subs command as follows:

> der := diff(p,x);
> subs(x=Pi/2,der);

Exercises

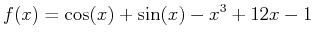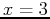1. Find the equation of the line tangent to the graph of the function $$f(x)=\cos(x)+\sin(x)-x^3+12x-1$$ at $x=3$. When calculating the derivative at a point, use the 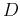$D$ command. Include a plot of the function and the tangent line on the same graph over the interval $0 \leq x \leq 5$.

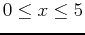2. For the same function $$f(x)=\cos(x)+\sin(x)-x^3+12x-1$$,
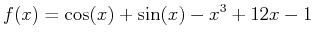   1. Plot 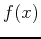$f(x)$ over the interval 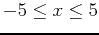$-5 \leq x \leq 5$ and state how many horizontal tangent lines to the graph there are.
   2. Plot the derivative of 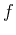$f$ over the same interval. Explain how this supports your answer above.
   3. Using the fsolve command along with labels, find each 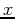$x$ value where a horizontal tangent line is located. Find the corresponding 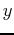$y$ values by plugging each 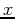$x$ value back into the function. State in text all points on the graph of 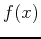$f(x)$ where the tangent line is horizontal.

3. The tangent line to a function at a particular value of x intersects the graph of the function at least once, at the point of tangency. However, the tangent line may intersect the graph at other points. In this problem, we investigate whether the tangent line at one point can also be tangent to the graph at another point. For example, consider the function
   
   $$g(x) = (x^2-1)^2$$
   
   
   Show that the tangent line at $x=-1$ is also tangent to the graph at $x=1$.

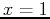   Next, suppose we change the function slightly.
   

   $$h(x) = (x^2-1)^2 +x/2$$
   
   
   Is it still possible to find two different values of 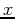$x$ such that the tangent lines coincide? The answer is yes. Find them.

4. Find the equation of the tangent line to
   
   $$f(x) = 4x^3+8x^2-24x+1$$
   
   
   at the point 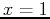$x=1$. Find another point on the graph that has the same slope as this point. Find the equation of the line tangent to 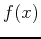$f(x)$ at this point. Plot the function and both tangent lines on the same graph.