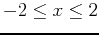Subsections

• Exercises

Higher Order Derivatives

The derivative represents the slope of a function. It can also represent the instantaneous velocity. The second derivative represents the acceleration and can also represent the concavity of a function. In order to calculate these and any other higher order derivative in Maple the commands D and diff are used. For the function 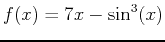$f(x)=7x-\sin^3(x)$ the second and third derivative will be calculated using both commands.

> f:=x->7*x^3-sin(x)^3;
> plot(f(x), x=-2..2);
> (D@@2)(f)(x);
> D[1,1](f)(x);
> diff(f(x),x,x);
> diff(f(x),x$2);

The 2 in the first D command stands for the second derivative. The 1 in the second D command means ``with respect to x''.

> (D@@3)(f)(x);
> D[1,1,1](f)(x);
> diff(f(x),x,x,x);
> diff(f(x),x$3);

In order to substitute an 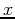$x$ value into the higher order derivative the subs command must be used for diff; but for D the 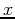$x$ value can be incorporated into the command itself.

> evalf(subs(x=0,diff(f(x),x,x,x)));
> (D@@3)(f)(0);
> D[1,1,1](f)(0);

Remember from your work with the first derivative that the D command cannot be used with expressions.

> g:=19*x^5-14*x+100;
> D(g)(x);
> diff(g,x);

Exercises

1. Given the function:
   
   $$f(x)=2\cos(x)-\frac{x^5}{5}-10$$
   
   

   A.

   Enter as a function

   B.

   Plot the function on the interval $-2\leq x \leq 2$

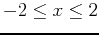
   C.

   Find the fifth order derivative using the D command.

   D.

   Find the fifth order derivative using the diff command.

   E.

   Plot the second derivative. About where does the second derivative graph cross the x-axis? Knowing that the second derivative represents concavity explain why your second derivative plot makes sense in conjunction with the plot of the original function.

2. A ball is thrown upward and its distance in feet is given as a function of seconds.
   
   $$s(t)=6+80t-16t^2$$
   
   

   A.

   Enter the function

   B.

   What is the initial velocity of the ball?

   C.

   When will the ball reach its maximum height?

   D.

   What is the highest point?

   E.

   What is the acceleration at any time?