$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

Applications of the Derivative

Purpose

In this lab we will use the first and second derivatives to study the monotonicity and concavity of various functions and determine their maxima and minima.

Examples

We will first start with a few examples

1. Consider the function

  > g:=x->x^2+16*x^2/(8-x)^2;

$\begin{maplelatex} \begin{displaymath} g := x\rightarrow x^{2} + 16\,{\displaystyle \frac {x^{2}}{(8 - x )^{2}}} \end{displaymath}\end{maplelatex}$

a. Find the local extrema for x<8 and for x>8.

For this we will compute the first derivative and determine the critical points

  > gprime:=x->D(g)(x);

$\begin{maplelatex} \begin{displaymath} {\it gprime} := x\rightarrow 2\,x + 32\,{... ...32\,{\displaystyle \frac {x^{2}}{(8 - x)^{3}}} \end{displaymath}\end{maplelatex}$

Next we could proceed in two ways:

1.: We could factor the derivative and determine the critical points and the sign of the derivative and then apply the first derivative test
2.: We could just find where the derivative cancels, and compute the second derivative at those points and then apply the second derivative test

Let's try both.

1. We factor g'

  > factor(gprime(x));

$\begin{maplelatex} \begin{displaymath} 2\,{\displaystyle \frac {x\,( - 640 + 192\,x - 24\,x^{2} + x^{3}) }{( - 8 + x)^{3}}} \end{displaymath}\end{maplelatex}$

This did not really work well since we know that a third order polynomial has at least one real solution and should therefore be factored further. We will try to force MAPLE to factor using irrational numbers (read the help for "factor").

  > factor(gprime(x),2^(1/3));

$\begin{maplelatex} \begin{displaymath} 2\,{\displaystyle \frac {x\,(x - 8 - 4\,2... ... 32\,2^{1/3} + 16\,2^{2/3})}{( - 8 + x)^{3 }}} \end{displaymath}\end{maplelatex}$

It seems that this worked better. However we are still not sure why Maple did not factor the quadratic polynomial. Is it because it does not have real solutions or because Maple is stupid?

We can check by solving the quadratic equation:

  > solve(x^2-16*x+4*2^(1/3)*x+64-32*2^(1/3)+16*2
^(2/3),x);

$\begin{maplelatex} \begin{displaymath} - 2\,2^{1/3} + 8 + 2\,I\,\sqrt{3}\,2^{1/3}, \, - 2\,2^{1/3} + 8 - 2\,I\,\sqrt{3}\,2^{1/3}\end{displaymath}\end{maplelatex}$

so Maple was not stupid after all! The roots are not real indeed! Thus the critical points are 0 and 8+4*2^(1/3).

When x > 8 the only critical point is 8+4*2^(1/3) and the derivative goes from being negative to being positive. Thus, by the "First Derivative Test Theorem" the function has a local minimum at

x=8+4*2^(1/3)

When x < 8 the only critical point is 0 and the derivative goes from being negative to being positive. Thus, by the "First Derivative Test Theorem" the function has a local minimum at x=0.

2. We will try now to apply the second derivative test.

For this we need the second derivative.

  > gdoubleprime:=x->D(gprime)(x);

$\begin{maplelatex} \begin{displaymath} {\it gdoubleprime} := x\rightarrow 2 + {\... ...96\,{\displaystyle \frac {x^{2}}{(8 - x)^{4}}} \end{displaymath}\end{maplelatex}$

We now need to compute the values of the second derivative at the critical points

  > gdoubleprime(0);

$\begin{maplelatex} \begin{displaymath} {\displaystyle \frac {5}{2}} \end{displaymath}\end{maplelatex}$

  > gdoubleprime(8+4*2^(1/3));

$\begin{maplelatex} \begin{displaymath} - 6 - 3\,2^{1/3} + {\displaystyle \frac {3}{32}} \,(8 + 4\,2^{1/ 3})^{2}\,2^{2/3}\end{displaymath}\end{maplelatex}$

Do you know if this is positive or not? Maple should know!

  > evalf(gdoubleprime(8+4*2^(1/3)));

$\begin{maplelatex} \begin{displaymath} 15.52440631\end{displaymath}\end{maplelatex}$

Since both are positive we can conclude that at both points the function has local minima.

b. Determine the intervals where the function is concave up and where it is concave down

This means that we have to determine the sign of the second derivative. We will factor it first

  > factor(gdoubleprime(x));

$\begin{maplelatex} \begin{displaymath} 2\,{\displaystyle \frac {5120 - 1792\,x +... ...\,x^{2} - 32\,x^{3} + x^{4}}{( - 8 + x)^{4}}} \end{displaymath}\end{maplelatex}$

So again it did not work; a fourth order polynomial should factor. We will try to force Maple again to use irrational numbers.

  > factor(gdoubleprime(x),2^(1/3));

$\begin{maplelatex} \begin{displaymath} 2\,{\displaystyle \frac {5120 - 1792\,x +... ...\,x^{2} - 32\,x^{3} + x^{4}}{( - 8 + x)^{4}}} \end{displaymath}\end{maplelatex}$

This did not work either. The only trick left is to find the solutions for g''(x)=0

  > solve(5120-1792*x+384*x^2-32*x^3+x^4);

$\begin{maplelatex} \begin{displaymath} 4\,{\rm RootOf}(20 - 28\,{\it \_Z} + 24\,{\it \_Z}^{2} - 8\,{\it \_Z}^{3} + {\it \_Z}^{4})\end{displaymath}\end{maplelatex}$

This did not work either... are you frustrated? So am I!

Let's try to force Maple to factor over the complex set

  > factor(5120-1792*x+384*x^2-32*x^3+x^4,complex);

$\begin{maplelatex} \begin{eqnarray*} \lefteqn{(x - 2.674884553 + 4.042070725\,I)... ...54161888\,I)\,(x - 13.32511545 - 6.354161888\,I)\end{eqnarray*}\end{maplelatex}$

So finally something worked. Let us analyze what we have: a product of four terms, that give us the four roots of the polynomial. The roots are two pairs of complex conjugate numbers. If we multiply the first two polynomials we get a quadratic polynomial with real coefficients, with a negative discriminant. This means that the polynomial has always the same sign, which coincides with the sign of x², namely it is positive. The same if we multiply the other two polynomials.

We can conclude that the second derivative has both the denominator and the numerator positive and that g is concave up everywhere.

c.Plot the function and see on the graph the local extrema and the intervals of concavity.

  > plot(g(x),x=-10..10);

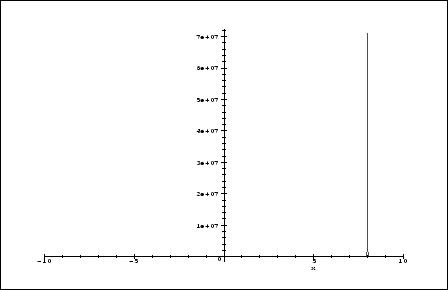
$\mapleplot {lab31001.eps}$

Ooops! This wasn't a good try. We cannot see anything on this graph. This is because at x=8

the function is not defined and as x approaches 8 the fuction have very large values. Therefore

we need to limit the range for y.

  > plot(g(x),x=-10..20,y=-2..1000);

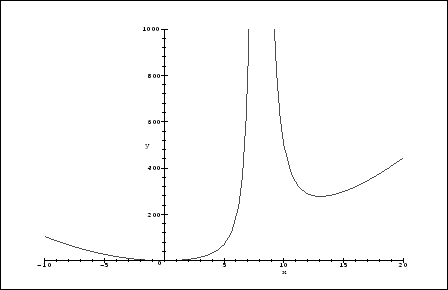
$\mapleplot {lab31002.eps}$

This shows us that indeed the function is always concave up and the local minima are at the two

points we determined above.

Remark. In some of the exercises below we will have to use the "non-principal root function" surd(x,n). Check the help page to see the definition for the case when x is real. Then try to plot x^(1/3) with and without using the surd function:

  > plot(x^(1/3),x=-10..10);

  > plot(surd(x,3),x=-10..10);

Exercises

1.

Determine by using the first or second derivative tests, the local minima and local maxima for the functions:

(a): x²/(x²+1)
(b): x^(2/3)*(1-x)
(c): x/(x²-1)^(1/3)

Plot the graph of each of the above functions.

2.

Determine the intervals of concavity and the points of inflexion of the graphs of the following functions

(a): x³/(x²+12)
(b): 4*x³-12*x
(c): (4*x³-12*x)^(1/5)

Plot the graph of each of the above functions.

$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

William W. Farr
2/24/1999