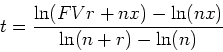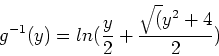Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The simple model for growth is
exponential growth, where
it is assumed that
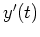 is proportional to
is proportional to 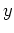 . That is,
. That is,
Separating the variables and integrating, we have
so that
In the case of exponential growth, we can drop the absolute value
signs around 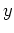 , because
, because 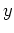 will always be a positive quantity.
Solving for
will always be a positive quantity.
Solving for 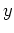 , we obtain
, we obtain
which we may write in the form 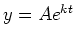 , where
, where 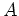 is an
arbitrary positive constant. The same formula is used for exponential decay, except the decay constant
is an
arbitrary positive constant. The same formula is used for exponential decay, except the decay constant 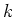 is negative.
is negative.
Suppose you invest a principal amount 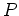 at an interest rate
at an interest rate 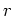 and want to compute the future value
and want to compute the future value 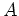 after
after 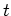 years. Assuming that the interest is compounded once a year, the future value of the investment would be given by the formula
years. Assuming that the interest is compounded once a year, the future value of the investment would be given by the formula
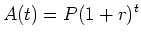 . When the interest is compounded more frequently, say
. When the interest is compounded more frequently, say 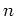 times per year, then formula for the future value of the investment would be
times per year, then formula for the future value of the investment would be
If the case of continuous compound interest or
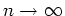 , then the future value of the investment would be
, then the future value of the investment would be
Now suppose you start with your initial investment 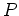 and add to that by making a regular investment of
and add to that by making a regular investment of 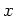 dollars per compound period. Then the future value
dollars per compound period. Then the future value 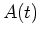 after
after 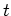 years with interest rate
years with interest rate 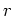 compounded
compounded 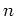 times per year is given by the formula:
times per year is given by the formula:
Suppose you want to figure out how long it would take to reach a desired future value, let's call it 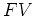 . Then solving the above equation for
. Then solving the above equation for 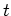 would give how many years
would give how many years 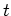 it would take to reach this amount making regular investments of
it would take to reach this amount making regular investments of 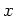 dollars per compound period with interest rate
dollars per compound period with interest rate 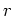 compounded
compounded 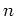 times per year.
times per year.
The main functions you need are the natural exponential and
natural logarithm. The Maple commands for these functions are
exp and ln. Here are a few examples.
> A:=t->P*(1+r/n)^(n*t);
> subs({P=50,r=0.06,n=12},A(10));
> A:=t->P*exp(r*t);
> subs({P=50,r=0.06},A(10));
> A:=t->x*((1+r/n)^t-1)/(r/n);
> subs({x=50,r=0.06,n=1},A(10));
> t_yrs:=(ln(FV*r+n*x)-ln(n*x))/(ln(n+r)-ln(n));
> subs({FV=1000,r=0.06,x=50,n=1},t_yrs);
Consider the functions 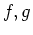 defined by
defined by
To be able to get an inverse the function must be one-to-one. You can plot the
functions to get a hint as to whether they are invertible or not.
> f:=x->exp(x)+exp(-x);
> plot(f(x),x=-5..5);
> g:=x->exp(x)-exp(-x);
> plot(g(x),x=-5..5);
Both satisfy the vertical-line test but 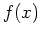 is not invertible since it does
not satisfy the horizontal-line test. Indeed
is not invertible since it does
not satisfy the horizontal-line test. Indeed 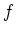 is not one-to-one, for instance
is not one-to-one, for instance
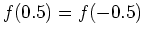 . From the plot it seems that the function
. From the plot it seems that the function 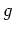 is one-to-one.
In order to determine its inverse we solve for x.
is one-to-one.
In order to determine its inverse we solve for x.
> solve(g(x)=y,x);
We observe that one of the solutions is not defined since the arguement of the logarithm can only be positive. Thus:
> ginv:=y->ln(y/2+sqrt(y^2+4)/2);
Let's look at the plot along with the line 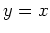 to see if our functions seem to make sense.
to see if our functions seem to make sense.
> plot({x,g(x),ginv(x)},x=-20..20,y=-20..20,scaling=constrained);
Let's check that we have computed the right inverse. By definition the composot
ion of the functions should be the line 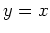 since an inverse is the reflectio
n about this line.
since an inverse is the reflectio
n about this line.
> g(ginv(y));
> simplify(%);
> ginv(g(x));
> simplify(%);
We are having difficulty getting 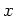 for the last composition. Think about what
issue the computer has in dealing with this simplification as you will come across this in the exercises.
for the last composition. Think about what
issue the computer has in dealing with this simplification as you will come across this in the exercises.
- Caclulate the future value of an ivestment of $1,500. earning 4.75% interest over a 9 year period using the formula for compound interest that compounds the interest for each of the following: yearly, semi-anually, quarterly, monthly, daily, hourly, and continuously. Explain what you observe.
- Use Maple's solve command to verify the formula in the background that calculates the time
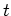 in years that it would take to reach a desired future value
in years that it would take to reach a desired future value 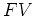 making regular payments of
making regular payments of 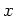 dollars per compound period, compounded
dollars per compound period, compounded 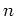 times per year with interest rate
times per year with interest rate 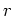 .
.
- Use this formula to approximate the number of years it would take to save $50,000 if you invested $1200 per year with an average rate of return at 3.5% compounded yearly.
-
- A)
- Plot the function
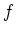 over the interval
over the interval
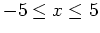 and plot the function
and plot the function 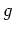 over the interval
over the interval
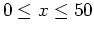 . Which function is not invertible and why?
. Which function is not invertible and why?
- B)
- Find the inverse of the invertible function.
- C)
- Plot the function and its inverse along with the line
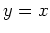 on the domain of
on the domain of
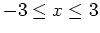 .
.
- D)
- Show that you have the correct inverse by using the composite definition. (When
you come across a simplifying problem and have figured out why the computer won't simplify ask your lab instructor how to bypass this problem.)



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2006-10-03
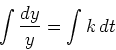
![\begin{displaymath}A(t) = \frac{x\left[(1+\frac{r}{n})^t-1\right]}{r/n}\end{displaymath}](img20.png)