


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to use Maple to study applications of
exponential and logarithmic functions. These are used to model many
types of growth and decay.
The simple model for growth is exponential growth, where
it is assumed that
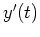 is proportional to
is proportional to 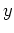 . That is,
. That is,
Separating the variables and integrating (see section 4.4 of the text),
we have
so that
In the case of exponential growth, we can drop the absolute value
signs around 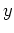 , because
, because 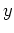 will always be a positive quantity.
Solving for
will always be a positive quantity.
Solving for 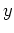 , we obtain
, we obtain
which we may write in the form 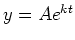 , where
, where 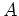 is an
arbitrary positive constant.
is an
arbitrary positive constant.
In a sample of a radioactive material, the
rate at which atoms decay is proportional to the amount of material present.
That is,
where 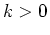 is a constant. This is the same equation as in exponential growth,
except that
is a constant. This is the same equation as in exponential growth,
except that 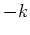 replaces
replaces 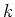 . The solution is
. The solution is
where 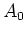 is a positive constant. Physically,
is a positive constant. Physically, 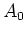 is the amount of
material present at
is the amount of
material present at 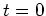 .
.
Radioactivity is often expressed in terms of an element's half-life.
For example, the half-life of carbon-14 is 5730 years. This statement means
that for any given sample of
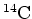 , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is 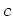 years, it must be
that
years, it must be
that
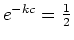 , so that
, so that 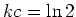 and
and
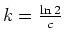 .
.
What is usually called Newton's law of cooling is a simple model for
the change in temperature of an object that is in contact with an
environment at a different temperature. It says that the rate of
change of the temperature of an object is proportional to the
difference between the object's temperature and the temperature of the
environment. Mathematically, this can be expressed as the differential
equation
where 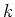 is the constant of proportionality and
is the constant of proportionality and
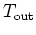 is
the temperature of the environment. Using a technique called
separation of variables it isn't hard to derive the solution
is
the temperature of the environment. Using a technique called
separation of variables it isn't hard to derive the solution
where 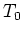 is the temperature of the object at
is the temperature of the object at 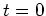 .
.
Information can be thought of as of a physical quantity which can be measured. According to the Gallup Institute, information news diffuses through a fixed adult population of size 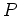 at a rate of time proportional to the number of people who have not heard the news.
at a rate of time proportional to the number of people who have not heard the news.
If 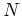 is the number of people who have heard the news after t days, then
is the number of people who have heard the news after t days, then
The initial condition 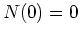 yields the solution
yields the solution
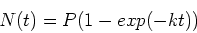
- An example of common logarithms is the decibel scale, particularly used for measuring loudness. (The decibel unit is named in honor of Alexander G. Bell (1847-1922), inventor of the telephone.) If
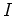 is the intensity of sound in watts per square meter, the decibel level of the sound is
is the intensity of sound in watts per square meter, the decibel level of the sound is
where 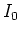 is an intensity corresponding roughly to the faintest sound that can be heard.
When tuning the rock band's equipment before the concert in a big concert hall, an audio engineer finds that in order to maintain appropriate loudness in this hall, he needs to increase the power of the amplifiers in comparison with the level used for the previous concert in a hall of smaller size.
is an intensity corresponding roughly to the faintest sound that can be heard.
When tuning the rock band's equipment before the concert in a big concert hall, an audio engineer finds that in order to maintain appropriate loudness in this hall, he needs to increase the power of the amplifiers in comparison with the level used for the previous concert in a hall of smaller size.
- What does the doubling the intensity add to the level of loudness in decibels?
- By what factor
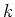 will the engineer have to multiply the intensity of the sound to add 20 to the sound level for the next concert of the band on the stadium?
will the engineer have to multiply the intensity of the sound to add 20 to the sound level for the next concert of the band on the stadium?
- Exponential growth can be used to model the growth of a certain kind of investments. Suppose that the value
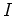 of an investment satisfies the differential equation
of an investment satisfies the differential equation
where 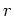 is the interest rate. If the interest rate is
is the interest rate. If the interest rate is 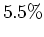 per year and you start with an investment of $12,000, how many years does it take to double? How many years does it take to quadruple? Is there an easy way to answer the second part of this question? Explain.
per year and you start with an investment of $12,000, how many years does it take to double? How many years does it take to quadruple? Is there an easy way to answer the second part of this question? Explain.
- A thermometer registered
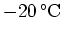 outside and then was brought into the house where the temperature was
outside and then was brought into the house where the temperature was
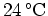 . After 5 minutes, it registered
. After 5 minutes, it registered
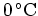 . When will it register
. When will it register
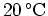 ?
?
- Suppose that 75% of a freshman class of 500 students on a campus heard about the market crash on Wall Street 3 days after it happened. How long will it take for 99% of the freshman to hear the news?



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2008-10-07
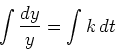
![]() , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is ![]() years, it must be
that
years, it must be
that
![]() , so that
, so that ![]() and
and
![]() .
.
![]() is the number of people who have heard the news after t days, then
is the number of people who have heard the news after t days, then
![]() yields the solution
yields the solution