The command to use is shown below.
> int(x^2,x=0..4);
Notice that Maple gives an exact answer, as a fraction. If you want a decimal approximation to an integral, you just put an evalf command around the int command, as shown below.
> evalf(int(x^2,x=0..4));
To compute an indefinite integral with Maple, you just leave out the range for the limits of integration, as shown below.
> int(x^2,x);Note that Maple does not include a constant of integration.
You can also use the Maple int command with functions or
expressions you have defined in Maple.
For
example, suppose you wanted to find area under the curve of the
function
![]() on the
interval
on the
interval ![]() . Then you can define this function in Maple with
the command
. Then you can define this function in Maple with
the command
> f := x -> x*sin(x);and then use this definition as shown below.
> int(f(x),x=0..Pi);
You can also simply give the expression corresponding to ![]() a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged to choose one or the other, so you don't
mix the syntax up.
a
label in Maple, and then use that label in subsequent commands as
shown below. However, notice the difference between the two
methods. You are urged to choose one or the other, so you don't
mix the syntax up.
> p := x*sin(x); > int(p,x=0..Pi);If you want to find the area bounded by the graph of two functions, you should first plot both functions on the same graph. You can then find the intersection points using either the solve or fsolve command. Once this is done, you can calculate the definite integral in Maple. An example below illustrates how this can be done in Maple by finding the area bounded by the graphs of
> f := x-> -x^2+4*x+6;
> g := x-> x/3+2;
> plot({f(x),g(x)},x=-2..6);
> a := fsolve(f(x)=g(x),x=-2..0);
> b := fsolve(f(x)=g(x),x=4..6);
> int(f(x)-g(x),x=a..b);
> int(-16*t^2+100*t,t=1..5)/(5-1);
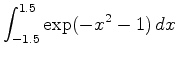
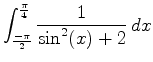
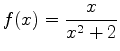 and
and
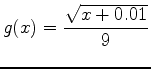 .
.
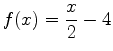 and
and