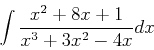Subsections

• Purpose
• Rational Functions
• Partial Fractions
• Exercises

Rational Functions and Partial Fractions

Purpose

The purpose of this lab is to show how quotient functions can be integrated.

Rational Functions

When a function is the quotient of two polynomials, you can easily take the integral if the numerator is the derivative of the denominator.

$$f(x)=\frac{6x+6}{x^2+2x+9}$$

> diff(x^2+2*x+9,x);

Note that the numerator times a constant is the derivative of the denominator.

> simplify((6*x+6)/(2*x+2));

Therefore, 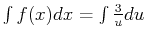$\int f(x) dx = \int \frac{3}{u} du$ which is an easy natural log integral.

> int(3/u,u);
> subs(u=x^2+2*x+9,int(3/u,u));

To check the work, let Maple do the intgral directly.

> int((6*x+6)/(x^2+2*x+9),x);

Remember with indefinite integrals the solution adds a constant. So, the inetgral solution is 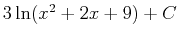$3 \ln(x^2+2x+9) +C$. Often a function is not in that straight forward form. With long division, you can try and get the quotient function into the form of a polynomial plus a fraction where the numerator is a derivative of the denominator: $polynomial+\frac{(constant)(derivative_{of} denominator)}{denominator}$. For example if

$$f(x)=\frac{x^3+x^2+x-1}{x^2+2x+2}$$

First execute long division and find the quotient and remainder.

> q:=quo((x^3+x^2+x-1),(x^2+2*x+2),x);
> r:=rem((x^3+x^2+x-1),(x^2+2*x+2),x);

The new form of the function is:

> f:=q+r/(x^2+2*x+2);

Note that the fractional part has the numerator a derivative times a constant 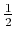$\frac{1}{2}$ of the denominator.

> diff(x^2+2*x+2,x);
> simplify(r/diff(x^2+2*x+2,x));
> int(q,x)+subs(u=x^2+2*x+2,int(1/(2*u),u));

To check the work, let Maple do the integral directly.

> int((x^3+x^2+x-1)/(x^2+2*x+2),x);

Remember to add a constant to the indefinite integral answer: $\frac{x^2}{2}-x+\frac{\ln(x^2+2x+2)}{2}+C$.

Partial Fractions

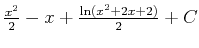When the function is a fraction with a denominator that can be factored into linear components then the partial method can be easily used.

$$g(x)=\frac{5x-1}{x^2-1}$$

The denominator is easily factored:

> factor(x^2-1);

So, 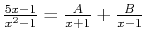$\frac{5x-1}{x^2-1}=\frac{A}{x+1}+\frac{B}{x-1}$. Multiplying by the common denominator and expanding gives:

> expand(5*x-1=A*(x-1)+B*(x+1));

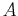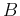With this equation we can solve for $A$ and $B$ by equating the coefficients of the x term and then equating the constants. This will give us two equations which can be solved simultaneously.

> solve({5*x=A*x+x*B,-1=-A+B},{A,B});

These values tell us that: 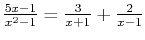$\frac{5x-1}{x^2-1}=\frac{3}{x+1}+\frac{2}{x-1}$. The right-hand side shows fractions that are easily integrated with the natural log.

> int(3/(x+1)+2/(x-2),x);

To check the work let Maple do the integral directly.

int((5*x-1)/(x^2-1),x);

Remember the constant: $2 \ln(x-1)+3 \ln(1+x) +C$.

Exercises

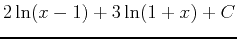Evaluate each of the following definite integrals below using long division and/or partial fractions. Show all steps and include plenty of text to keep your work clear. Also check your final answer by having Maple do the integral directly.

1. 
   
   $$\int \frac{x^5+2x^3+1}{x^2+x} dx$$
   
   

2. 
   
   $$\int \frac{x^2+8x+1}{x^3+3x^2-4x} dx$$