


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
There are two main ways to think of the definite integral. The easiest
one to understand is as a means for
computing areas (and volumes). The second way the definite integral is
used is as a sum. That is, we use the definite integral to ``add
things up''. Here are some examples.
- Computing net or total distance traveled by a moving object.
- Computing average values, e.g. centroids and centers of mass,
moments of inertia, and averages of probability distributions.
This lab is intended to introuduce you to Maple commands for approximating and computing integrals, including applications of integrals.
Suppose 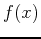 is a non-negative, continuous function defined on some
interval
is a non-negative, continuous function defined on some
interval ![$[a,b]$](img2.png) . Then by the area under the curve
. Then by the area under the curve 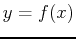 between
between
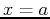 and
and 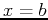 we mean the area of the region bounded above by the
graph of
we mean the area of the region bounded above by the
graph of 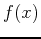 , below by the
, below by the 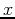 -axis, on the left by the vertical
line
-axis, on the left by the vertical
line 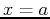 , and on the right by the vertical line
, and on the right by the vertical line 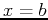 . All of the
numerical methods in this lab depend on subdividing the interval
. All of the
numerical methods in this lab depend on subdividing the interval
![$[a,b]$](img2.png) into subintervals of uniform length.
into subintervals of uniform length.
In these simple rectangular approximation methods, the area above each
subinterval is approximated by the area of a rectangle, with the height of the
rectangle being chosen according to some rule. In particular, we will
consider the left, right and midpoint rules.
The Maple student package has commands for visualizing these
three rectangular area approximations. To use them, you first must
load the package via the with command. Then try the three commands
given below to help you understand the differences between the
three different rectangular approximations. Note that
the different rules choose rectangles which in
each case will either underestimate or overestimate the area.
> with(student):
> rightbox(x^2,x=0..4,8);
> leftbox(x^2,x=0..4,8);
> middlebox(x^2,x=0..4,8);
To commands below show how to approximate the area under the curve 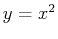 using the left-endpoint rule in Maple
using the left-endpoint rule in Maple
> f:=x->x^2;
> h:=(4-0)/8;
> h*(f(0)+f(0.5)+f(1)+f(1.5)+f(2)+f(2.5)+f(3)+f(3.5))
The basic Maple command for computing definite and indefinite
integrals is the int command.
To compute the indefinite integral
with Maple:
> int(x^2,x);
Note that Maple does not include a constant of integration.
Suppose you wanted to compute the following definite
integral with Maple.
The command to use is:
> int(x^2,x=0..4);
If you want to find the area bounded by the graph of two functions, you should first plot both functions on the same graph. You can then find the intersection points using either the solve or fsolve command. Once this is done, you can calculate the definite integral in Maple. An example below illustrates how this can be done in Maple by finding the area bounded by the graphs of
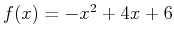 and
and 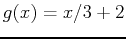 :
:
> f := x-> -x^2+4*x+6;
> g := x-> x/3+2;
> plot({f(x),g(x)},x=-2..6);
> a := fsolve(f(x)=g(x),x=-2..0);
> b := fsolve(f(x)=g(x),x=4..6);
> int(f(x)-g(x),x=a..b);
- Plot
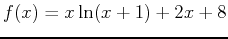 over the interval
over the interval ![$[-1,5]$](img13.png) . Approximate the area under
. Approximate the area under 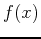 , above the
, above the 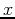 -axis over the given interval using right-endpoint and midpoint rules with 6 rectanglesusing the Riemann Sum formula and again using Maple's rightsum and middlesum command. Then use an integral to calculate the exact area and state which approximation was better, right-endpoint rule or midpoint rule.
-axis over the given interval using right-endpoint and midpoint rules with 6 rectanglesusing the Riemann Sum formula and again using Maple's rightsum and middlesum command. Then use an integral to calculate the exact area and state which approximation was better, right-endpoint rule or midpoint rule.
- Find the area of the region bounded by the curves
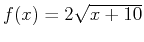 and
and
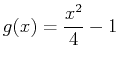 . Include a plot of the region bounded by the given curves.
. Include a plot of the region bounded by the given curves.
- Find the area of the region bounded by the curves
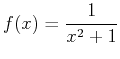 and
and
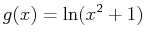 . Include a plot of the region bounded by the given curves.
. Include a plot of the region bounded by the given curves.
- Find the area of the region bounded by the curves
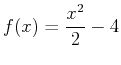 and
and
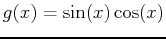 . Include a plot of the region bounded by the given curves.
. Include a plot of the region bounded by the given curves.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2018-09-07
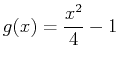 . Include a plot of the region bounded by the given curves.
. Include a plot of the region bounded by the given curves.
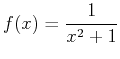 and
and
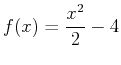 and
and