Subsections

• Purpose:
• Background:
• Exercises

The Inverse Trigonometric Functions

Purpose:

The purpose of this lab is to increase your familiarity with the inverse trigonometric functions.

Background:

The inverse trigonometric functions are examples of transcendental functions. The trigonometric functions are not one to one functions and hence their inverses are not functions. However, as indicated in your text, we can restrict the domain of the trigonometric functions so that the resulting inverse functions are indeed functions.

The inverse trigonometric functions arise in problems that require finding angles from side measurements in triangles. They also provide antiderivatives for a wide variety of functions and hence appear in solutions to a number of differential equations that arise in mathematics, engineering and physics.

Some of the Maple commands that you will need to know are as follows:

In order to use the inverse trigonometric functions you must place arc before the 3 letter symbol for each. For example

arccos(x)is the command for inverse cosine;
arcsin(x)is the command for inverse sine;
arctan(x)is the command for inverse tangent;
arcsec(x)is the command for inverse secant;
arccsc(s)is the command for inverse cosecant;
arccot(x)is the command for inverse cotangent.

Defining x

  > x:=0.785

the corresponding value of the inverse tangent can be found as

  > evalf(arctan(x));

Remember from previous labs we can take the derivative using either of the following commands

  > diff(arcsec(x),x);

or we can use the D operator with functions

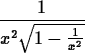
  > f:=x->arccsc(x);

  > D(f)(x);

We can take the indefinite integral by the following command. Try the following:

  > int(arccsc(x),x);

Exercises

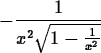
Exercise I:(Definitions, Graphs, Properties)

1a.

Graph each of the following trigonometric functions (sin, cos, tan) and their corresponding inverse function on the same graph. Restrict the domain of each trigonometric function so that the corresponding inverse function is defined.

1b.

Compute the following values.

a.

$arccos(\sqrt{2}/2$)

b.

arcsin(1/2)

c.

arctan(a).

2.

From 1 above note that the graph of the inverse sine function is symmetric about the origin. This implies the function is odd. Show graphically that $\sin^{-1}(-x) = -\sin^{-1}(x)$.

3.

Compute and graph the derivative of inverse sine function and the derivative of inverse cosine function.

(a)

Knowing the type of symmetry of the inverse sine function, what type of symmetry should its derivative have? Does the graph of the derivative of inverse sine function agree?

(b)

How do the graphs of the inverse functions appear to be related? What transformations can you apply to the graph of the inverse sin function to obtain the graph of the inverse cos function? What effect do these transformations have on the graph of the derivative of inverse sin function? Knowing the derivative of the inverse sin function, what is a reasonable prediction for the derivative of the inverse cos function?

Exercise II:(Applications)

1.

A billboard to be built parallel to a highway will be 12 m high with its bottom 4 m above the eye level of the average passing motorist. How far from the highway should the billbord be placed to maximize the vertical angle it subtends at the motorist's eyes? Note that some degree of interpretation is necessary once a numerical answer has been derived. Can you explain why?

2.

Use inverse trigonometric functions to prove that the vertical angle subtended by a rectangular painting on a wall is greatest when the painting is hung with its center at the level of the observer's eye.

3.

Evaluate the following integrals and support graphically:

(a)