$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

Planar Domains and Solids of Revolution

Introduction

The purpose of this lab is to use Maple to study planar domains and the solids of revolution. Solids of revolution are created by rotating curves in the x-y plane about an axis, generating a three dimensional object. They are discussed in Chapter 6 of Calculus by Varberg and Pursell (sections 2 and 3). The specific properties of them that we wish to study are their volume, surface area, and graph.

Background

If we have a curve lying entirely on or above the x-axis, which is the graph of a function y = f(x), and x is restricted to being between a and b, then we may rotate it about the x-axis, generating a three dimensional object, a solid of revolution.

For example, if the curve is simply f(x) = ax/h (a straight line) and x is between and h, we obtain a cone of height h and radius a.

Consider f(x) = x² + 1 for $-2 \leq x \leq 2,$ which appears in Figure 1.

**Figure 1:** Plot of f(x)=x²+1.
$\begin{figure} \centerline{ \psfig {file=volrev_fig1.ps,height=4.0in,width=2.0in,angle=-90} }\end{figure}$

If we take the region between the graph of f(x) and the x-axis and revolve it about the x-axis then it becomes the surface of the solid pictured in Figure 2.

**Figure 2:** Solid generated by rotating f(x)=x²+1 about the x-axis.
$\begin{figure} \centerline{ \psfig {file=volrev_fig2.ps,height=4.0in,width=2.5in,angle=-90} }\end{figure}$

If f(x) = x^1/2 and x is between, say, and 1, we obtain a bowl shaped object called a paraboloid. (Note the equation y = x^1/2 is equivalent to x = y², a parabola).

If f(x) = (a² - x²)^1/2 and x is between -a and a, we obtain a sphere of radius a (since the equation y = (a² - x²)^1/2 is equivalent to x² + y² = a², a circle of radius a).

The area of the region R below the graph of the function $y = f(x) \geq 0,\;\;x \epsilon [a,b]$ , and above the x-axis is given by
$\begin{maplelatex} \begin{displaymath} A = \int^b_a f(x)dx\end{displaymath}\end{maplelatex}$
(see p. 263). The region R is bounded by the curve involving the curvilinear part $y = f(x),\;\;x \epsilon[a,b],$ the horizontal base [a,b] with length b - a, and two vertical segments with lengths f(a) and f(b). The length P of the curvilinear part of the boundary is given by
$\begin{maplelatex} \begin{displaymath} P = \int^b_a \sqrt{1+[f^\prime(x)]^2}dx \end{displaymath}\end{maplelatex}$
(see p. 321).

The volume of the solid obtained by rotating the curve $y = f(x),\;x \epsilon [a,b]$ about the x-axis is given by

$\begin{maplelatex} \begin{displaymath} V = \pi \int_a^b [f(x)]^2 \, dx \end{displaymath}\end{maplelatex}$
(see Example 4a on page 316 of the textbook for illustration)

The volume is obtained by adding up volumes of cylindrical disks, while its surface area (p. 324) is given by
$\begin{maplelatex} \begin{displaymath} S = 2\pi \int_a^b f(x)\{1 + [f'(x)]^2\}^{1/2} \, dx \end{displaymath}\end{maplelatex}$
Note that both of these formulas are for rotating the graph of f(x) about the x-axis.

Area Radius and Perimeter Radius of Planar Domain

We will consider planar domains ${\cal D}$ defined as a union of the region R introduced above and the region $R_\ast$ produced by reflection of R in the x-axis. Clearly, the area of ${\cal D}$ equals 2A, and the perimeter of ${\cal D}$ equals 2[P + f(a) + f(b)]. Particularly, if the region R is defined as the interior of a half of the ellipse
$\begin{maplelatex} \begin{displaymath} y = f(x) = \frac{1}{2} \sqrt{1-x^2},\;\;x \epsilon [-1,1],\end{displaymath}\end{maplelatex}$
belonging to the upper half plane y > 0 then $R_\ast$ becomes the interior of a half of the reflected ellipse
$\begin{maplelatex} \begin{displaymath} y = -\frac{1}{2} \sqrt{1-x^2},\;\;x \epsilon [-1.1],\end{displaymath}\end{maplelatex}$
belonging to the lower half plane y < 0. So, ${\cal D} = R\cup R_\ast$ - a complete ellipse, and its area is equal to 2A, whereas its perimeter equals 2P since f(a) = f(b) = 0 in this case.

The area radius $\bar{A}$ of the planar domain ${\cal D}$ is defined as the radius of the circle possessing the same area as ${\cal D}$ , i.e.
$\begin{maplelatex} \begin{displaymath} \bar{A} = \left(\displaystyle\frac{2A}{\pi}\right)^{1/2}.\end{displaymath}\end{maplelatex}$
The perimeter radius $\bar{P}$ of the planar domain is defined as the radius of the circle having the same perimeter as ${\cal D}$ , i.e.
$\begin{maplelatex} \begin{displaymath} \bar{P} = \displaystyle\frac{P+f(a)+f(b)}{\pi}.\end{displaymath}\end{maplelatex}$

Volume Radius and Surface Radius

The volume radius $\bar{V}$ of the body is defined as the radius of the sphere possessing the volume V, i.e.
$\begin{maplelatex} \begin{displaymath} \bar{V} = \left(\displaystyle\frac{3V}{4\pi} \right)^{1/3}.\end{displaymath}\end{maplelatex}$

The surface radius $\bar{S}$ of the body is defined as the radius of the sphere having the surface area S, i.e.
$\begin{maplelatex} \begin{displaymath} \bar{S} = \left(\displaystyle\frac{S}{4\pi}\right)^{1/2}.\end{displaymath}\end{maplelatex}$

Graphics Through Maple

To plot the graph of the function y = f(x) given by the list of points $[x_1,y_1], [x_2,y_2], \ldots$ we use the command plot in the relevant format, e.g.

  > plot([[5,5],[6,7],[7,10],[8,12]]);

Check it!

To do graphics in three dimensions, we utilize the tubeplot function from the plots library of Maple, along with suitable options.

For sake of demonstration, suppose we wish to plot the surface of revolution one gets from rotating the curve $y = x^{1/2} + 1, \;\; 0 \leq x \leq 9$ about the x-axis. Maple commands to accomplish this would be:

  > f:= x -> sqrt(x) + 1;

$\begin{maplelatex} \begin{displaymath} {f} := {x} \rightarrow {\rm sqrt}(\,{x}\,) + 1\end{displaymath}\end{maplelatex}$

  > with(plots):
PltStyle:= axes= NORMAL, style= PATCHNOGRID, tubepoints=40;

$\begin{maplelatex} \begin{displaymath} {\it PltStyle} := {\it axes}={\it NORMAL}... ... style}={\it PATCHNOGRID}, {\it tubepoints}=40\end{displaymath}\end{maplelatex}$

  > tubeplot([x,0,0], x=0..9, radius=f(x),PltStyle);

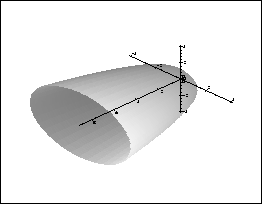
$\begin{figure} \centerline{ \psfig {file=goulet.ps,height=2.5in,width=2.0in,angle=-90} }\end{figure}$

The last command uses the function tubeplot from the plots library, rotating about the x-axis (as controlled by the first argument, [x,0,0], letting x range from to 9, using the function f(x) to determine the radius at each point, and setting the options as set up by the line assigned PltStyle). The only especially noteworthy thing set by PltStyle is the last option, tubepoints. This effectively determines the resolution of the graph; the higher the value, the smoother it is (but the longer it takes). A value as low as 10 gives a fairly crude surface, by comparison. (Try it!)

Finding Volumes of Revolution

Since this involves straightforward integration, one may simply issue commands such as:

  > f:= x-> sqrt(x) +1;

$\begin{maplelatex} \begin{displaymath} {f} := {x} \rightarrow {\rm sqrt}(\,{x}\,) + 1\end{displaymath}\end{maplelatex}$

  > vol:= Int(Pi*f(x)^2, x=0..9);

$\begin{maplelatex} \begin{displaymath} {\it vol} := \int^9_0 \pi(\sqrt{x} + 1)^2dx\end{displaymath}\end{maplelatex}$

  > evalf(vol);

$\begin{maplelatex} \begin{displaymath} 268.6061719\end{displaymath}\end{maplelatex}$

Surface Area

Assuming the function has been defined, one might issue:

  > S:= Int(2*Pi*f(x)*sqrt(1+D(f)(x)^2), x= 0..9);

$\begin{maplelatex} \begin{displaymath} {S} := {\displaystyle \int_{0}^{9}} { \pi... ...t {4 + {\displaystyle \frac {1}{{x}}} }\,{d}{x}\end{displaymath}\end{maplelatex}$

  > evalf(S);

$\begin{maplelatex} \begin{displaymath} 178.5614656\end{displaymath}\end{maplelatex}$
to find the surface area of the solid obtained by rotating f(x) about the x-axis.

Exercises

For the function,
$\begin{maplelatex} \begin{displaymath} y = f(x) = \displaystyle\frac{1}{2}\sqrt{1-x^2},\;\; x \epsilon [-1,1],\end{displaymath}\end{maplelatex}$
the graph in the (x,y) plane is a half of ellipse; revolving this graph about the x-axis, we generate an ellipsoid of revolution.

1.

(a): Plot the graph of y = f(x).
(b): Find the area A of the planar domain R.
(c): Find the length P of a half of the ellipse.
(d): Calculate the area radius $\bar{A}$ and the perimeter radius $\bar{P}$ for the ellipse ${\cal D} = R\cup R_\ast$ and make sure that
$\begin{maplelatex} \begin{displaymath} m = \displaystyle\frac{\bar{A}}{\bar{P}} < 1.\end{displaymath}\end{maplelatex}$
(e): Consider the family of half-ellipses
$\begin{maplelatex} \begin{displaymath} y = f(x) = k\sqrt{1-x^2},\;\;x \epsilon [-1,1]\end{displaymath}\end{maplelatex}$
depending on parameter k. This parameter will be assumed taking the values from the interval $\left[\displaystyle\frac{1}{3}, 3\right]$ .
(f): Calculate $\bar{A}$ and $\bar{P}$ for the ellipses ${\cal D} = R\cup R_\ast$ related to the following set of values of parameter k:
$\begin{maplelatex} \begin{displaymath} k = 1/3,\;\;\;k = 1/2,\;\;\;k = 3/4,\;\;\;k = 1,\;\;\;k = 2,\;\;\;k = 3,\end{displaymath}\end{maplelatex}$
and plot the graph of the ratio
$\begin{maplelatex} \begin{displaymath} m(k) = \displaystyle\frac{\bar{A}(k)}{\bar{P}(k)}\end{displaymath}\end{maplelatex}$
versus k.

2.

(a): Plot the surface of the ellipsoid defined above.
(b): Find the volume V of this ellipsoid.
(c): Find the area S of the surface of this ellipsoid.
(d): Calculate the volume radius $\bar{V}$ and the surface radius $\bar{S}$ and make sure that
$\begin{maplelatex} \begin{displaymath} n = \displaystyle\frac{\bar{V}}{\bar{S}} < 1.\end{displaymath}\end{maplelatex}$
(e): Consider the family of ellipsoids generated by rotating the half-ellipses
$\begin{maplelatex} \begin{displaymath} y = f(x) = k\sqrt{1-x^2},\;\;x \epsilon [-1,1]\end{displaymath}\end{maplelatex}$
about the x-axis; here k is the parameter taking the values from the interval $\left[\displaystyle\frac{1}{3}, 3\right]$ .
(f): Calculate $\bar{V}$ and $\bar{S}$ for the ellipsoids related to the following set of values of parameter k:
$\begin{maplelatex} \begin{displaymath} k = 1/3,\;\;\;\;k = 1/2,\;\;\;\;k = 3/4,\;\;\;\;k = 1,\;\;\;\;k = 2,\;\;\;\;k = 3,\end{displaymath}\end{maplelatex}$
and plot the graph of the ratio
$\begin{maplelatex} \begin{displaymath} n(k) = \displaystyle\frac{\bar{V}(k)}{\bar{S}(k)}\end{displaymath}\end{maplelatex}$
versus k.

3.

Given the graph of n = n(k), what can you say about the ellipsoid of revolution for which n(k) attains its maximum value? What is this maximum value? Make a plausible hypothesis related to the maximum value of n(k) calculated for all convex bodies, not necessarily the solids of revolution. (We call convex the bodies that contain along with any two points the whole segment bounded by these points.) Develop similar consideration for the graph of m = m(k) and the relevant elliptical domains in the plane.

$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

Jane E Bouchard
9/14/1998