$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

Applications of Exponential and Logarithmic Function

Purpose

The purpose of this lab is to give you experience in dealing with exponential and logarithmic functions appeared in various applied problems.

The lab consists of Background including both the relevant theoretical notes and description of the use of appropriate Maple commands. There are four problems, each of which has separate preliminary remarks (discussion of equations, introduction of terms, etc.) and an exercise to do.

Background

Theoretical Notes

Exponential growth and decay. In many natural processes the rate of change of physical quantity (velocity, temperature, amount of money, electric current, whatever) is proportional to the current amount of the quantity. If we also know the amount present at time t=0, call it y₀, we can find y as a function of t by solving the following initial value problem:

Differential equation: 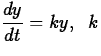$\displaystyle\frac{dy}{dt} = ky,\;\; k$ is a constant.
(1)
Initial conditions: y = y₀ when t = 0 .

If y is positive and increasing, then k is positive, and we use Eq. (1) to say that the rate of growth is proportional to what has already been accumulated. If y is positive and decreasing, then k is negative, and Eq. (1) is used to say that the rate of decay is proportional to the amount still left.

It is seen that the constant function y = 0 is a solution of Eq. (1). To find the non-zero solutions, the equation is solved in accordance with the known technique of separating variables and integrating (see [Varberg & Purcell, Calculus, p.372]). The solution of the initial value problem is
$\begin{maplelatex} \begin{displaymath} y = y_0e^{kt}.\hspace*{3.5in}{(2)}\end{displaymath}\end{maplelatex}$

The constant y₀ is the value of the function at t=0. The constant k is called the growth rate in exponential growth (k >0) and the decay rate in exponential decay (k < 0). In a process that can be modeled by exponential functions, the rate constant k depends only on the process and the conditions under which it is carried out.

Some processes are described by differential equations similar to (1) but containing two or more constants characterizing some other circumstances in which these processes are carried out. Also, the initial conditions might be specified by more complicated expressions. The corresponding initial value problems lead to the solution having slightly different form, e.g., like (2) including a combination of additive and multiplicative constants. You will meet illustrations of that in the problems below.

In some applications, a quantity y demonstrates exponential growth or decay on a huge range. To make this quantity more convenient in handling, special scales involving logarithms are used. This allows to deal with the corresponding powers instead of actual values of y .

Relevant Maple Means. In order to enter the exponential and natural log functions, the exp and ln command should be used. The syntax of these commands is similar to that of sin and cos. For example, below it is shown how to enter the function f(x) = e^x and then evaluate it at x = 0.7.

  > f:=exp(x);

$\begin{maplelatex} \begin{displaymath} f :=e^x\end{displaymath}\end{maplelatex}$

  > evalf(subs(x=0.7, f));

$\begin{maplelatex} \begin{displaymath} 2.013752707\end{displaymath}\end{maplelatex}$

In the same manner, the function $g(x) = \ln(x)$ is used:

  > g := ln(x);

$\begin{maplelatex} \begin{displaymath} g := \ln(x)\end{displaymath}\end{maplelatex}$

  > evalf(subs(x=0.7, f));

$\begin{maplelatex} \begin{displaymath} -.3566749439\end{displaymath}\end{maplelatex}$

To simplify expression involving logarithms, use command simplify; it works as follows:

  > simplify(exp(a+ln(b*exp(c))));

$\begin{maplelatex} \begin{displaymath} be^{a+c}\end{displaymath}\end{maplelatex}$

The common logarithm is defined by function log10 = log[10], but log10 must be defined with the command readlib(log10) before use:

  > readlib(log10): log10(10000);

$\begin{maplelatex} \begin{displaymath} \displaystyle\frac{\ln(10000)}{\ln(10)}.\end{displaymath}\end{maplelatex}$

Maple manipulates with common logarithms the same way but may return expressions including natural logarithms.

The solve command is usually sufficient for solving most probelms encountered in your Calculus courses. This command comes in a couple of varieties, as shown below.

i.

Solve linear equation:

> solve (y=m*x+b,x);

$\begin{maplelatex} \begin{displaymath} \displaystyle\frac{y - b}{m}\end{displaymath}\end{maplelatex}$

ii.

Solve displaying result as an equation:

  > solve (34-2*x=12*x+6,x);

$\begin{maplelatex} \begin{displaymath} \{x = 2\} \end{displaymath}\end{maplelatex}$

Plotting the two functions f(x) = e^x and $g(x) = \ln x$ on the same coordinate system illustrates an idea of the symmetry around the line y=x. All the three graphs can be plotted by the use of the following command:

  > plot([f,g,x], x=-4..4, y=-4..4);

**Figure 1:**
$\begin{figure} \centerline{ \psfig {file=logpic.ps,height=4.0in,width=2.0in,angle=-90} }\end{figure}$

In order to get a graph of a left-hand/right-hand side of an equation obtained after symbolic transformations and/or computations, first use commands lhs and rhs respectively. The example:

  > eq1 := A=b+c*exp(k*t): eq2 := subs(b=2.5,c=3,k=0.8,eq1):

  > rh2 := rhs(eq2):

  > plot(rh2, t=0..3);

Problem 1: Radioactive Decay

Preliminary remarks

Radioactive decay is a typical example to which the exponential decay model can be applied. In Eq. (2), y represent the mass (in grams) of an isotope, y₀ and k are constants determining from initial conditions: y₀ is the mass present originally, and k is the decay constant.

k is often specified in terms of an empirical parameter, the half-life of the isotope. The half-life $\tau$ of a sample of a radioactive isotope is the time required for half of the atoms of that sample to decay. The half-lives of some common radioactive isotopes are as follows:

Figure 1:
Uranium (U-238) 4,510,000,000 years

Plutonium (Pu-239) 24,360 years

Carbon (C-14) 5,730 years

Einsteinium (Es-254) 270 days

Nobelium (No-257) 23 sec

**Figure 1:**
Uranium (U-238)	4,510,000,000 years
Plutonium (Pu-239)	24,360 years
Carbon (C-14)	5,730 years
Einsteinium (Es-254)	270 days
Nobelium (No-257)	23 sec

The relationship between k and $\tau$ is set up from the condition actually saying that the sample of y₀ grams will contain only $\displaystyle\frac{1}{2}y_0$ grams after the time $\tau$ , so that, referring (2):
$\begin{maplelatex} \begin{displaymath} \displaystyle\frac{1}{2} = e^{-k\tau}\end{displaymath}\end{maplelatex}$
and therefore:
$\begin{maplelatex} \begin{displaymath} \tau = \displaystyle\frac{\ln 2}{k }.\end{displaymath}\end{maplelatex}$

Exercise

The worst nuclear accident in history happened in 1986 at the Chernobyl nuclear plant near Kiev in the Ukraine. An explosion destroyed one of the plant's four reactors, releasing large amount of radioactive isotopes into the atmosphere.

Consider 10 grams of the plutonium isotope Pu-239 released in the Chernobyl nuclear accident.

1.: How long will it take for the 10 grams to decay to 1 gram?
2.: Plot the graph showing the decay of the mass of the plutonium isotope took place up to date (1986-1998). Does it look like a typical curve of exponential decay(Fig.1)? Why? Discuss the graph in the context of the radioactive safety.

Problem 2: Information Diffusion

Preliminary remarks

You may think of information as of a physical quantity which can be measured. In accordance with the Gallup Institute, information news diffuse through an adult population of fixed size P at a time rate proportional to the number of people who have not heard the news.

If N(t) is the number of people who have heard the news after t days, then
$\begin{maplelatex} \begin{displaymath} \displaystyle\frac{dN}{dt} = k(P - N) \hspace*{3.5in}{(3)}\end{displaymath}\end{maplelatex}$
The obvious fact that N(0) = 0 serves here as the initial condition, thus the solution of the initial value problem is given by
$\begin{maplelatex} \begin{displaymath} N(t) = P(1 - e^{-kt}) \hspace*{3.5in}{(4)}\end{displaymath}\end{maplelatex}$

Exercise

3 days after the August 31 market crisis on the Wall Street, a poll of WPI freshmen showed that 77% had heard about it.

1.: How long will it take for 99% of the WPI freshmen to hear about the Black Monday?
2.: Plot the graph illustrating the diffusion of the news about the market crisis through the WPI freshmen as the function of time. From the graph, estimate how many students would be aware of the Black Monday after 5 and 7 days?

Problem 3: Newton's Law of Cooling

Preliminary remarks

An aluminum beam brought from the outside cold into a machine shop where the regular normal temperature is maintained warms up to the temperature of the surrounding air. A hot silver ingot immersed in water cools to the temperature of the surrounding water.

In situations like these, the rate at which an object's temperature is changing at any given time is approximately proportional to the difference between its temperature and the temperature of the surrounding medium. This observation is sometimes called the Newton's Law of Cooling, although, as in the case with the aluminum beam, it applies to warming as well.

An equation representing this law can be written as
$\begin{maplelatex} \begin{displaymath} T - T_s = (T_0 - T_s)e^{-kt},\hspace*{2.8in}{(5)}\end{displaymath}\end{maplelatex}$
where T is the temperature of the object at time $t, \;T_s$ is the surrounding temperature, T₀ is the value of T at time zero.

Exercise

A cup of coffee is taken from a coffeemaker at 98 $^\circ$ C and left on the office table. In the air-conditioned office, the temperature is held at 20 $^\circ$ C. After 5 minutes, the coffee's temperature is 38 $^\circ$ C.

1.: How much longer will it take the coffee to loose its taste quality, i.e., to cool down to the temperature of 22 $^\circ$ C?
2.: Assume the coffee is left on the table of an outside cafe on a hot summer day when the temperature is 35 $^\circ$ C and on a cold winter day when the temperature is 5 $^\circ$ C. Get the expression for the coffee temperature as a function of time for these cases in form (5).
3.: Plot the graphs T versus t for the all three environments using the same coordinate axes.
4.: From the graphs, make an estimate when the coffee should be drunk in each situation (in office, in winter cafe, in summer cafe) if the coffee is supposed to be best at temperature 60 $^\circ$ C.

Problem 4:Logarithmic scale

Preliminary remarks

Base 10 logarithms, often called common logarithms, appear in many scientific and applied formulas.

For example, earthquake intensity is often reported on the logarithmic Richter scale. Here the formula is
$\begin{maplelatex} \begin{displaymath} \mbox{Magnitude } R = \log_{10}\left(\dis... ...yle\frac{a}{T}\right) + B, \hspace*{2.3in}{(6)}\end{displaymath}\end{maplelatex}$
where a is the amplitude of the ground motion in microns at the receiving station, T is the period of the seismic wave in seconds, and B is an empirical factor that allows for the weakening of the seismic wave with increasing distance from the epicenter of the earthquake. For an earthquake 10,000 km from the receiving station, B = 6.8. Thus if the recorded vertical ground motion is a = 10 microns and the period is T = 1 sec, the earthquake's magnitude, following (6), is R = 7.8. An earthquake of this magnitude does great damage near its epicenter.

Another example of the use of common logarithms is the decibel scale using, particularly, for measuring loudness. (The decibel unit is named in honor of Alexander G. Bell (1847-1922), inventor of the telephone.) If I is the intensity of sound in watts per square meter, the decibel level of the sound is
$\begin{maplelatex} \begin{displaymath} \mbox{sound level} = 10\log_{10}(I/I_0),\mbox{ dB},\end{displaymath}\end{maplelatex}$
where I₀ is an intensity of 10^-12 watts per square meter corresponding roughly to the faintest sound that can be heard.

Exercise

When tuning the rock band's equipment before the concert in a big concert hall, an audio engineer finds that in order to maintain appropriate loudness in this hall, he needs to increase the power of the amplifiers in comparison with the level used for the previous concert in the hall of less size.

1.: Find what does the doubling the power add to the level of loudness in decibels.
2.: By what factor k will the engineer have to multiply the intensity of I of the sound to add 10 to the sound level for the next concert of the band on the stadium?

$next$ $up$ $previous$
Next: About this document ... Up: Labs and Projects for Previous: Labs and Projects for

Christine M Palmer
9/23/1998