


Next: About this document ...
Up: No Title
Previous: No Title
Subsections
The purpose of this lab is to use Maple to study exponential, logarithmic,
and logistic functions. These are used to model many types of growth, as
well as in many scales, such as the Richter and decibel scales.
Logarithmic Scale: The decibel scale is a logarithmic scale
used to measure sound. Measured at some point A, the measurement
of the sound in decibels is
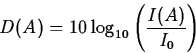
where I(A) is the sound intensity at the point A, and I0 is a
reference intensity chosen so that the threshold of human hearing is
approximately 0 decibels.
Exponential growth: The simplest model for growth is exponential, where
it is assumed that
y'(t) is proportional to y. That is,
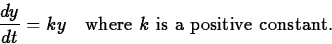
Separating the variables and integrating (see section 4.4 of the text),
we have
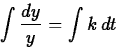
so that
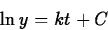
(If y is a positive quantity, we may drop the absolute value signs
around y.) Solving for y
y = ekt + C
which we may write in the form y = Aekt, where A is an arbitrary
positive constant. (Why?)
Exponential Decay: In a sample of a radioactive material, the
rate at which atoms decay is proportional to the amount of material present.
That is,
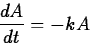
where k>0 is a constant. This is the same equation as in exponential growth,
except that -k replaces k. The solution is
A(t) = A0 e-kt
where A0 is a positive constant. Physically, A0 is the amount of
material present at t=0.
Radioactivity is often expressed in terms of an element's half-life.
For example, the half-life of carbon-14 is 5730 years. This statement means
that for any given sample of 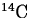 , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that 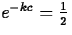 , so that
, so that 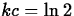 and
and 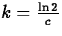 .
.
Logistic growth:
One of the consequences of exponential growth is that 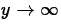 as
as 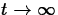 . However, in some situations there is a limit B
to how large y can get. For example, the population of bacteria in
a laboratory culture, where the food supply is limited. In such situations,
the rate of growth slows as the population reaches the carrying capacity.
One useful model is the logistic growth model. It assumes that
the rate of growth is proportional to the product of the population
and the difference between the population and its upper limit. Thus we
model the growth with the differential equation
. However, in some situations there is a limit B
to how large y can get. For example, the population of bacteria in
a laboratory culture, where the food supply is limited. In such situations,
the rate of growth slows as the population reaches the carrying capacity.
One useful model is the logistic growth model. It assumes that
the rate of growth is proportional to the product of the population
and the difference between the population and its upper limit. Thus we
model the growth with the differential equation
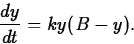
In the exercises you will use Maple to solve this equation and work with
an example.
- 1.
- Suppose element Z has a half-life of 2 years.
- (a)
- Choose an initial amount A0 for the element. Find the
amount as a function of time, and plot this function.
- (b)
- How long is it until the amount is
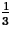 of what it was
initially?
of what it was
initially?
- (c)
- How long is it until the amount is
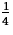 of what it was
initially?
Is there a quick way to answer this question?
of what it was
initially?
Is there a quick way to answer this question?
- 2.
- In 1935 Charles F. Richter of Cal Tech developed a scale for
measuring the magnitude of earthquakes. The Richter Scale formula is
given by
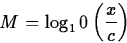
where M is the magnitude of the earthquake, x is the amplitude of
the largest seismic wave as measured on a standard seismograph 100
kilometers from the epicenter
and c is the amplitude of a reference earthquake of amplitude 1
micron ( 1 micron is 0.001 mm) on a standard seismograph at the same
distance from the epicenter.
- (a)
- When the amplitude of an eqrthquake is tripled, by how much does
the magnitude increase?
- (b)
- In 1989, the San Francisco Bay area suffered severe damage from
an earthquake of magnitude 7.1. However, the damage was not nearly as
extensive as that caused by the great quake of 1906, which has been
estimated to have had the magnitude 8.3. What is the ratio of the
amplitude of the 1906 quake to the 1989 quake?
- (c)
- The largest earthquake magnitude ever measured was 8.9 for an
earthquake in Japan in 1933. Determine the ratio of the amplitude of
this earthquake to that of the 1906 San Francisco earthquake.
- 3.
- Consider the logistic growth differential equation
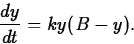
Separating the variables yields the equation
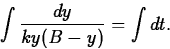
- (a)
- Use Maple to evaluate these integrals. Then use Maple's results to
solve the differential equation for y as a function of x. (Remember
that maple does not include a constant of integration in its answer, so you
will have to include it yourself. Note, also, that maple does not include
absolute-value signs when integrating
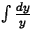 , so you may have
to modify the arguments of logarithms, to make sure that you are taking
the log of a positive number. Be sure to explain clearly what you are doing.)
, so you may have
to modify the arguments of logarithms, to make sure that you are taking
the log of a positive number. Be sure to explain clearly what you are doing.)
- (b)
- Explain how your answers to (a) may be written in the form
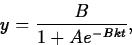
where A is some positive constant.
- (c)
- Suppose at time t=0 the population of bacteria in a culture is 1000,
and the limited environment can support no more than 100,000 bacteria.
After 1 hour the population is 5,000. Find the values of A and k.
Then plot y as a function of t. What is the population when the rate of
growth is most rapid?



Next: About this document ...
Up: No Title
Previous: No Title
Dina Solitro
9/28/1999
![]()
![]()
![]()
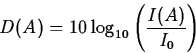
![]()
![]()
![]()
![]()
![]() , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is c years, it must be
that ![]() , so that
, so that ![]() and
and ![]() .
. ![]() as
as ![]() . However, in some situations there is a limit B
to how large y can get. For example, the population of bacteria in
a laboratory culture, where the food supply is limited. In such situations,
the rate of growth slows as the population reaches the carrying capacity.
One useful model is the logistic growth model. It assumes that
the rate of growth is proportional to the product of the population
and the difference between the population and its upper limit. Thus we
model the growth with the differential equation
. However, in some situations there is a limit B
to how large y can get. For example, the population of bacteria in
a laboratory culture, where the food supply is limited. In such situations,
the rate of growth slows as the population reaches the carrying capacity.
One useful model is the logistic growth model. It assumes that
the rate of growth is proportional to the product of the population
and the difference between the population and its upper limit. Thus we
model the growth with the differential equation
![]()
![]()
![]()
![]()
![]()