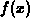 at the left-hand endpoint of the subinterval.
at the left-hand endpoint of the subinterval.
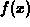 at the right-hand endpoint of the subinterval.
at the right-hand endpoint of the subinterval.
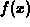 at the midpoint of the subinterval.
at the midpoint of the subinterval.
In these simple approximation schemes, the area above each subinterval is approximated by the area of a rectangle, with the height of the rectangle being chosen according to some rule. The rules we will be concerned with are as follows.
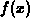 at the left-hand endpoint of the subinterval.
at the left-hand endpoint of the subinterval.
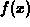 at the right-hand endpoint of the subinterval.
at the right-hand endpoint of the subinterval.
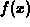 at the midpoint of the subinterval.
at the midpoint of the subinterval.
The Maple student package has commands for visualizing these three rectangular area approximations. To use them, you first must load the package via the with command. Then try the three commands given below. Make sure you understand the differences between the three different rectangular approximations.
> with(student):
> rightbox(x^2,x=0..4);
> leftbox(x^2,x=0..4);
> middlebox(x^2,x=0..4);
There are also Maple commands leftsum, rightsum, and middlesum to sum the areas of the rectangles, see the examples below. Note the use of evalf to obtain numerical answers.
> rightsum(x^2,x=0..4);

> evalf(rightsum(x^2,x=0..4));

> middlesum(x^2,x=0..4);

> evalf(middlesum(x^2,x=0..4));

It should be clear from the graphs that adding up the areas of the rectangles only approximates the area under the curve. However, by increasing the number of subintervals the accuracy of the approximation can be increased. All of the Maple commands described so far in this lab permit a third argument to specify the number of subintervals. The default is 4 subintervals. See the example below for the area under y=x from x=0 to x=2 using the rightsum command with 4, 10, 20 and 100 subintervals. (This area can be calculated to be exactly 2.) Try it yourself with the leftsum and middlesum commands.
> evalf(rightsum(x,x=0..2));

> evalf(rightsum(x,x=0..2,10));

> evalf(rightsum(x,x=0..2,20));

> evalf(rightsum(x,x=0..2,100));

In this example it appears that, as the number of subintervals increases, the rectangular apprroximation becomes more accurate. Of course, we realize that this is happening only because we knew from the start that the area of the triangular region being dealt with is 2. The next two sections describe ways of assessing the acuracy of some rectangular approximations.