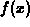 on the
subinterval.
on the
subinterval.
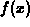 on the
subinterval.
on the
subinterval.
We introduce two more rectangular approximations.
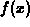 on the
subinterval.
on the
subinterval.
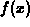 on the
subinterval.
on the
subinterval.
It should be clear that, if the area being approximated has A square units of area, then
lower sum 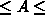 upper sum.
upper sum.
In general, it is rather complicated to compute upper and lower sums.
However, if 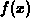 is monotonic, the situation is much easier. If
is monotonic, the situation is much easier. If
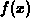 is increasing on the interval
is increasing on the interval 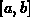 , then the upper sum is just
the right sum and the lower sum is just the left sum. In the last
example with
, then the upper sum is just
the right sum and the lower sum is just the left sum. In the last
example with 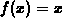 , the right sums (which are upper sums) moved
down toward the value of A as the number of subintervals increased.
What happens with the left sums (which are lower sums) as n, the
number of subintervals, increases?
, the right sums (which are upper sums) moved
down toward the value of A as the number of subintervals increased.
What happens with the left sums (which are lower sums) as n, the
number of subintervals, increases?