


Next: Exercises
Up: Background
Previous: Upper and lower
The midpoint rule with n subintervals (designated as 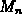 ) usually
gives better accuracy than either the left endpoint rule (
) usually
gives better accuracy than either the left endpoint rule (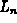 ) or
the right endpoint rule (
) or
the right endpoint rule (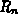 ). This means that, for a given n,
). This means that, for a given n,
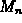 is generally closer to A than either
is generally closer to A than either 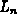 or
or 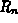 . In
numericcal analysis texts it is shown that the error,
. In
numericcal analysis texts it is shown that the error, 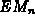 , in using
, in using
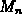 to approximate the area under
to approximate the area under 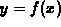 on
on 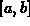 satisfies
satisfies
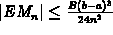
where B is the absolute maximum of 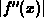 on
on 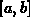 . In
practice, B is often approximated by a number N that is an upper bound
for B, that is B < N. For instance, if
. In
practice, B is often approximated by a number N that is an upper bound
for B, that is B < N. For instance, if 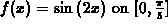 , N might be taken as 4. Do you see why? For more
complicated functions, Maple can be used to get a value for N that is
close to B.
, N might be taken as 4. Do you see why? For more
complicated functions, Maple can be used to get a value for N that is
close to B.
Note that the error bound formula gives a worst case estimate, the
accuracy achieved for a given n may be much better than the guarantee
given by the formula.
William W. Farr
Wed Nov 1 13:27:42 EST 1995
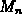 ) usually
gives better accuracy than either the left endpoint rule (
) usually
gives better accuracy than either the left endpoint rule (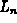 ) or
the right endpoint rule (
) or
the right endpoint rule (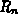 ). This means that, for a given n,
). This means that, for a given n,
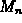 is generally closer to A than either
is generally closer to A than either 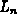 or
or 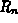 . In
numericcal analysis texts it is shown that the error,
. In
numericcal analysis texts it is shown that the error, 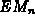 , in using
, in using
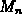 to approximate the area under
to approximate the area under 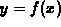 on
on 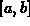 satisfies
satisfies
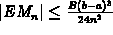
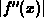 on
on 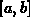 . In
practice, B is often approximated by a number N that is an upper bound
for B, that is B < N. For instance, if
. In
practice, B is often approximated by a number N that is an upper bound
for B, that is B < N. For instance, if 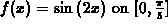 , N might be taken as 4. Do you see why? For more
complicated functions, Maple can be used to get a value for N that is
close to B.
, N might be taken as 4. Do you see why? For more
complicated functions, Maple can be used to get a value for N that is
close to B.