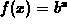 was introduced,
(for
was introduced,
(for 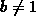 , b > 0) you saw that the function is increasing if
b > 1 and decreasing if b < 1. You can observe the monotonicity
by plotting
, b > 0) you saw that the function is increasing if
b > 1 and decreasing if b < 1. You can observe the monotonicity
by plotting 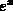 and
and 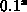 . Note that in Maple e is capitalized.
. Note that in Maple e is capitalized.
When the exponential function 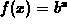 was introduced,
(for
was introduced,
(for 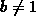 , b > 0) you saw that the function is increasing if
b > 1 and decreasing if b < 1. You can observe the monotonicity
by plotting
, b > 0) you saw that the function is increasing if
b > 1 and decreasing if b < 1. You can observe the monotonicity
by plotting 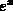 and
and 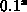 . Note that in Maple e is capitalized.
. Note that in Maple e is capitalized.
> plot(E^x,x=-1..1);
> plot((.1)^x,x=-1..1);
The logarithmic function 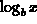 was introduced for
was introduced for 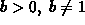 as the inverse of the exponential. The logarithm is therefore increasing if b > 1 and decreasing if 0 < b < 1.
Indeed you can plot
as the inverse of the exponential. The logarithm is therefore increasing if b > 1 and decreasing if 0 < b < 1.
Indeed you can plot 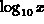 and
and 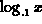 . Note that the
notation for
. Note that the
notation for 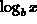 in Maple is: log[b]x.
in Maple is: log[b]x.
> plot(log[10](x),x=0.1..10);
> plot(log[0.1](x),x=0.1..10);
From the monotonicity properties you can compare two logarithms having the same base, without computing their values:
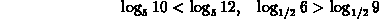
We can also see what is the behavior of the 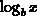 with b, for a fixed x. You can use ``animate'' to plot the family of functions
with b, for a fixed x. You can use ``animate'' to plot the family of functions
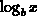 for different values of b.
for different values of b.
> with(plots):
> animate(log[b](x),x=0.1..10,b=1.1..10,frames=30);
> animate(log[b](x),x=0.1..10,b=0.01..0.1,frames=30);
In both animations you see that for a fixed x in the
interval 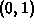
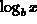 increases with b but for x in the
interval
increases with b but for x in the
interval 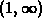 it decreases.
it decreases.
As a result you can now compare logarithms to different bases without computing their values:
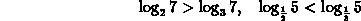
Here are some examples how you can use Maple to solve logarithmic and exponential equations. Solve:
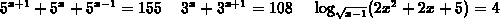
> solve(5^(x+1)+5^(x)+5^(x-1)=155,x);

> evalf(solve(3^x+3^(x+1)=108,x));

> solve(log[sqrt(x-1)](2*x^2+2*x+5)=4,x);

Observe that the command ``evalf'' makes Maple evaluate the result. Without it you get a result in terms of a logarithm.
You can also use Maple to differentiate and integrate exponential and logarithmic functions, as can be seen from the following examples.
Differentiate:
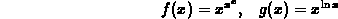
> diff(x^(x^x),x);
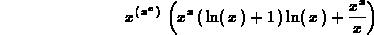
> diff(x^(ln(x)),x);

Use Maple to integrate:
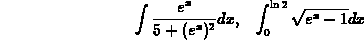
> int(E^x/(5+(E^x)^2),x);
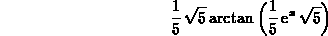
> int(sqrt(E^x-1),x=0..ln(2));
