Inverse functions

Consider the functions f, g defined for any real x by:

You can plot the functions to get a hint to whether they are invertible or not. on the interval .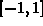

  > f:=x->E^x+E^(-x);

  > plot(f(x),x=-1..1);

  > g:=x->E^x-E^(-x);

  > plot(g(x),x=-1..1);

We observe that f is not invertible since it does not satisfy the horizontal line test. Indeed f is not one-to-one since, for instance, 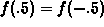. From the plot, it seems that the function g satisfies the horizontal line test. In order to determine its inverse, we solve for x:

  > solve(E^x-E^(-x)=y,x);

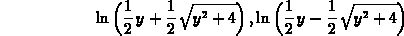
We observe that one of the solutions is not defined since the argument of the logarithm can only be positive. Thus:

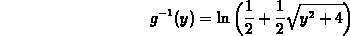
Let us check that we computed the right inverse. By definition

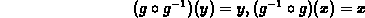
Indeed if we denote the inverse function by ginv and compose the functions we get:

  > ginv:=y->ln(1/2*y+1/2*sqrt(y^2+4));

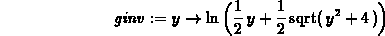
  > (g@ginv)(y);

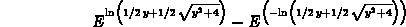
  > simplify((g@ginv)(y));

  > (ginv@g)(x);

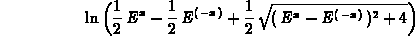
  > simplify((ginv@g)(x));

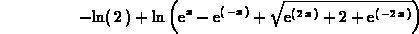
You have do some manipulations in the last output to obtain x !