Exercises

1.

a. Use Maple to compute the following integral:

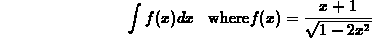
b. Use Maple to differentiate

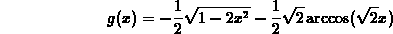
and ``simplify'' the result. You got back , although g is different from the answer you got in a. Explain why.

2.

Use Maple to solve for x in the equations:

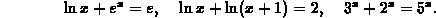
Are all the solutions acceptable? Use a monotonicity argument to show that the above equations cannot have more than one solution.

3.

Use Maple to determine the inverse of the function defined, for any real x, by:

(The above function is called the ``hyperbolic tangent'' and it is usually denoted by 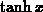. Its inverse is usually denoted by 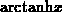or )

4.

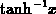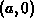
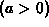A person standing in a plane at the origin, holds a taut rope of length a to which a weight is attached, initially at the point . The person walks along the positive y-axis, dragging the weight.

a. Determine the position of the person when the weight is at a point 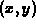. Determine the slope of the taut rope.

b. Find the equation 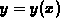of the path along which the weight moves by integrating the above slope.

c. Show that x=0 is a vertical asymptote for the path of the weight. (This means that the weight will never touch the y-axis!).