Subsections

• Introduction
• The integrate command in Maple
• More uses for Riemann sum approximations

Applications of the Definite Integral

Introduction

In the text, the lectures, and the previous lab, you have seen that two important problems--(a) finding the area under the graph of a positive function and (b) finding the position given the velocity--give rise to the definite integral as the limit of rectangular approximations. Definite integrals arise in many other contexts as well. It is an important skill to recognize when you can use Riemann sum approximations, and to set up the definite integral that results when you pass to the limit.

By the Fundamental Theorem of Calculus, you can evaluate defiinite integrals by antidifferentiating. Programs like Maple can antidifferentiate many functions automatically, and therefore are very helpful in doing definite integral problems.

The integrate command in Maple

Maple has two words for the integrate command, int and integrate. You can use them interchangeably; they both mean the same thing to Maple.

To find the indefinite integral (antiderivative) of f(x), you would execute the command integrate(f(x),x);

  > integrate(x^2+2*x, x);
  > integrate(a*x-x^2, x);
  > integrate(a*x-x^2, a);

Note that Maple does not include a constant of integration. If you are using the indefinite integral in a situation where the constant of integration is important, you must include it yourself.

For the definite integral, the limits of integration are included in the second argument:

  > integrate(x^2+2*x, x=0..1);    # note the similarity in
  > integrate(a*x-x^2, x=-1..2.5); # syntax to setting the
  > integrate(a*x-x^2, a=p..q);    # limits for a plot command.

It would be nice if the antiderivative of every elementary function were itself an elementary function. That is not, however, the case. If you give Maple a function whose antiderivative is not an elementary function, there are two types of outcomes.

It may happen that Maple can't figure out anything to do, and just returns the integral unevaluated:

  > integrate( sin(cos(x)),x);
  > integrate( cos(x^4 + 1),x);

Or, it may happen that Maple can express the answer in terms of functions not covered in a typical calculus course. You won't be responsible for knowing any of these functions, but you should be aware that they exist.

  > integrate( sqrt(2/Pi)*cos(x^2),x);
  > integrate( sin(x)/x,x);

More uses for Riemann sum approximations

As another example of a physical problem giving rise to a definite integral, suppose you want to find the mass of a wire of length L and a variable density p(x), where x is the distance from one end of the wire. If the density were a constant, the mass would be pL. Since the mass is not constant, we need to use a more refined approach.

Divide the wire (conceptually, not with a wirecutter) into n small pieces. If n is large, then we'd expect the density to be roughly constant within each piece, even though the density might vary considerably between pieces. So the density at a point x_k^* in the $k^{\hbox{\footnotesize th}}$ piece is fairly representative of the density at every point in that piece. Hence the mass of the $k^{\hbox{\footnotesize th}}$ piece is approximately $p(x_k^*)\Delta x_k$ where $\Delta x_k$ is the width of each piece. Our approximation for the total mass is

$$\sum_{k=1}^n p(x_k^*)\Delta x_k\;,$$

which is a Riemann sum. We now pass to the limit, by taking finer and finer partitions to the wire, obtaining the definite integral

$$\int_0^L p(x)dx.$$

Note that in obtaining the definite integral, you don't need to know details of how you divide the wire, how you pick the point at which to sample the density, or even what the density is. (The last, of course, is important in evaluating the definite integral.)

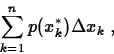
Being able to apply the above procedure as needed is much more valuable than memorizing formulas that result from the procedure in specific cases.